0 48789 48797 48803 48807 48813 48815 48819 48825 48827 48833 48839 48843 48845 48849 48855 48857 48863 48867 48869 48873 48875 48879 48881 48883 48884 48885 48887 48888 48889 48891 48893 48897 48899 48903 48905 48909 48915 48917 48923 48927 48929 48933 48939 48945 48947 48953 48957 48959 48965 48969 48975 48983 447348
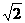 的正方形ABCD放在平面直角坐标系中,点A在坐标原点,点C在y轴的正半轴上,经过B、C、D三点的抛物线c1交x轴于点M、N(M在N的左边).
的正方形ABCD放在平面直角坐标系中,点A在坐标原点,点C在y轴的正半轴上,经过B、C、D三点的抛物线c1交x轴于点M、N(M在N的左边).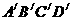 的中心G在点M上,
的中心G在点M上,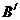 、
、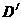 在x轴的负半轴上(
在x轴的负半轴上( 在第三象限,当点G沿着抛物线c1从点M移到点N,正方形随之移动,移动中
在第三象限,当点G沿着抛物线c1从点M移到点N,正方形随之移动,移动中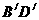 始终与x轴平行.
始终与x轴平行.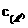 、
、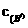 的函数关系式;
的函数关系式; ②如图3,当正方形
②如图3,当正方形
 求点G的坐标.
求点G的坐标.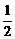 x2+4, M(
x2+4, M(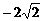 ,0),N(
,0),N(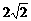 ,0)
,0) 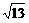 ,-3+
,-3+ )
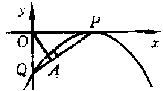
)  (2010年江苏省泰州市济川实验初中中考模拟题)已知抛物线
(2010年江苏省泰州市济川实验初中中考模拟题)已知抛物线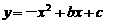 的部分图象如图所示.
的部分图象如图所示.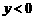 时,x的取值范围.
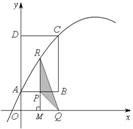
时,x的取值范围.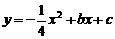 经过A、C两点.过点P作x轴的垂线,垂足为M,交抛物线于点R.设点P的运动时间为t(秒),△PQR的面积为S(平方单位).
经过A、C两点.过点P作x轴的垂线,垂足为M,交抛物线于点R.设点P的运动时间为t(秒),△PQR的面积为S(平方单位).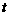 ≤5时,求S与t之间的函数关系式,并直接写出S的最大值.
≤5时,求S与t之间的函数关系式,并直接写出S的最大值.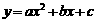 的顶点坐标为
的顶点坐标为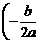 ,
,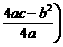 .]
.]
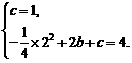 解得
解得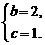
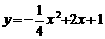 .
.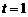 时,P点坐标为(1,1),∴Q点坐标为(2,0).
时,P点坐标为(1,1),∴Q点坐标为(2,0).
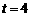 时,P点坐标为(2,3),∴Q点坐标为(5,0).
时,P点坐标为(2,3),∴Q点坐标为(5,0).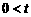 ≤2时,
≤2时,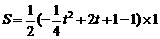 .
.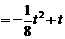 .
.
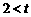 ≤5时,
≤5时,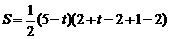 .
.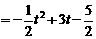 .
.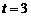 时,S的最大值为2.
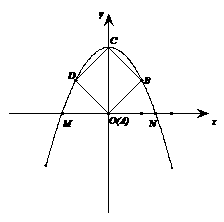
时,S的最大值为2.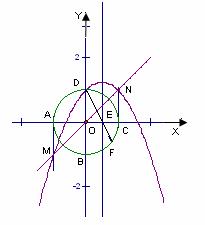 (2010年河南中考模拟题6)如图,在平面
(2010年河南中考模拟题6)如图,在平面 直角坐标系x0y中,半径为1的圆的圆心O在坐标原点,且与两坐标轴分别交于A、B、C、D四点。抛物线
直角坐标系x0y中,半径为1的圆的圆心O在坐标原点,且与两坐标轴分别交于A、B、C、D四点。抛物线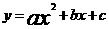 与y轴交于点D,与直线y=x交于点M、N,且MA、NC分别与圆O相切与点A和点C。
与y轴交于点D,与直线y=x交于点M、N,且MA、NC分别与圆O相切与点A和点C。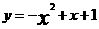 ,
,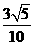 ,
,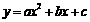 的图象的一部分如图所示.已知它的顶点M在第二象限,且经过点A(1,0)和点B(0,l).
的图象的一部分如图所示.已知它的顶点M在第二象限,且经过点A(1,0)和点B(0,l).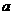 ,
,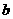 所满足的关系式;
所满足的关系式;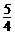 倍时,求a的值;
倍时,求a的值;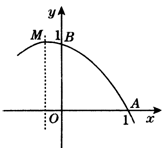 (3)是否存在实数a,使得△ABC为直角三角形.若存在,请求出a的值;若不存在,请说明理由.
(3)是否存在实数a,使得△ABC为直角三角形.若存在,请求出a的值;若不存在,请说明理由. :(1)将A(1,0),B(0,l)代入
:(1)将A(1,0),B(0,l)代入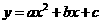 得
得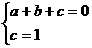 ,可得:
,可得: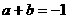
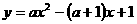 ,顶点M的纵坐标为
,顶点M的纵坐标为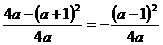 ,
, 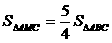 ,由同底可知:
,由同底可知: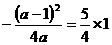 ,
,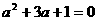 ,得:
,得: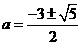
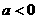 ,因为抛物线过点(0,1),顶点M在第二象限,其对称轴x=
,因为抛物线过点(0,1),顶点M在第二象限,其对称轴x=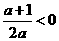 ,
, 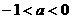 , ∴
, ∴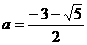 舍去,从而
舍去,从而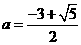
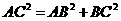 ,得:
,得: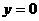 ,可得:
,可得: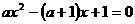 ,
,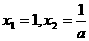
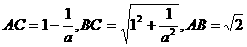
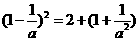 .
.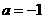 ,由-1<a<0,不合题意.所以不存在.
,由-1<a<0,不合题意.所以不存在.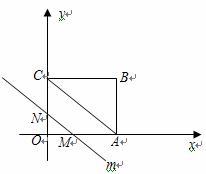
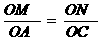 ,
,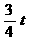 ,S=
,S=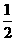 ×OM×ON=
×OM×ON=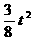 . (6分)
. (6分)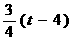 .(7分)
.(7分)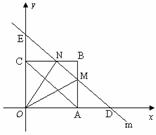 而△OND的高是3.
而△OND的高是3.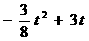 . ( 10分)
. ( 10分) 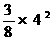 =6; (11分)
=6; (11分)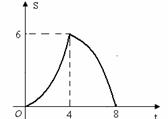 ∵ 抛物线S=
∵ 抛物线S=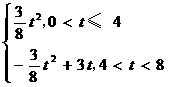
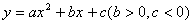
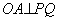 ,垂足为A,且
,垂足为A,且
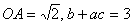
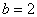
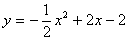
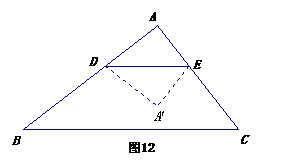 3.(2010年河南中考模拟题3)如图,在
3.(2010年河南中考模拟题3)如图,在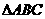 中,∠
中,∠
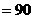 °,
°,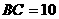 ,
, 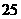 ,点
,点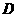 为
为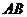 边上的任意一点(
边上的任意一点(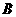 重合),过点
重合),过点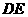 ∥
∥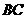 ,交
,交 于点
于点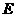 .设
.设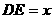 以
以 翻折,所得的
翻折,所得的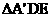 与梯形
与梯形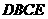 重叠部分的面积记为y.
重叠部分的面积记为y. ﹤
﹤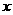 ≤
≤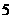 时y与x的函数关系式;
时y与x的函数关系式; 时y与x的函数关系式;
时y与x的函数关系式;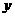 的值最大?最大值是多少?
的值最大?最大值是多少?
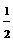 MN
MN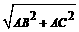 =5
=5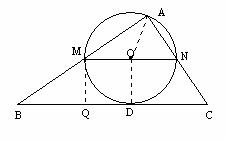 ∵MN∥BC,∴∠AMN=∠B,∠ANM=∠C
∵MN∥BC,∴∠AMN=∠B,∠ANM=∠C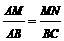 ,
,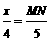 ,
,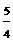 x, ∴OD=
x, ∴OD=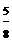 x
x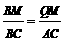 ,∴BM=
,∴BM=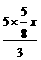 =
=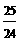 x,AB=BM+MA=
x,AB=BM+MA=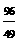
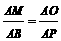 =
=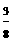 x2.
x2.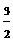
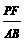 )2=
)2=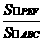
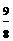 x2+6x-6
x2+6x-6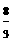 )2+2
)2+2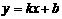 ,且
,且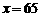 时,
时,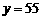 ;
;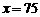 时,
时,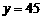 .
.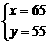
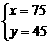 代入
代入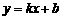 中
中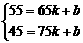
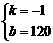 ∴
∴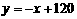
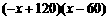
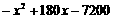
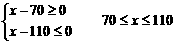
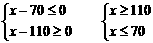 (舍去)
(舍去)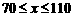 ,但
,但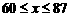 ∴
∴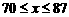
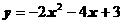 的顶点坐标是 .
的顶点坐标是 .