14、(2007山东临沂)某工程机械厂根据市场需求,计划生产A、B两种型号的大型挖掘机共100台,该厂所筹生产资金不少于22400万元,但不超过22500万元,且所筹资金全部用于生产此两型挖掘机,所生产的此两型挖掘机可全部售出,此两型挖掘机的生产成本和售价如下表:
|
型号 |
A |
B |
|
成本(万元/台) |
200 |
240 |
|
售价(万元/台) |
250 |
300 |
(1)该厂对这两型挖掘机有哪几种生产方案?
(2)该厂如何生产能获得最大利润?
(3)根据市场调查,每台B型挖掘机的售价不会改变,每台A型挖掘机的售价将会提高m万元(m>0),该厂应该如何生产可以获得最大利润?(注:利润=售价-成本)

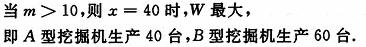
13、(2007四川眉山)某县响应“建设环保节约型社会”的号召,决定资助部分付镇修建一批沼气池,使农民用到经济、环保的沼气能源.幸福村共有264户村民,政府补助村里34万元,不足部分由村民集资.修建A型、B型沼气池共20个.两种型号沼气池每个修建费用、可供使用户数、修建用地情况如下表:
|
沼气池 |
修建费用(万元/个) |
可供使用户数(户/个) |
占地面积(m2/个) |
|
A型 |
3 |
20 |
48 |
|
B型 |
2 |
3 |
6 |
政府相关部门批给该村沼气池修建用地708m2.设修建A型沼气池x个,修建两种型号沼气池共需费用y万元.
(1)求y与x之间的函数关系式;
(2)不超过政府批给修建沼气池用地面积,又要使该村每户村民用上沼气的修建方案有几种;
(3)若平均每户村民集资700元,能否满足所需费用最少的修建方案.

12、(2007南充)某商店需要购进一批电视机和洗衣机,根据市场调查,决定电视机进货量不少于洗衣机的进货量的一半.电视机与洗衣机的进价和售价如下表:
|
类 别 |
电视机 |
洗衣机 |
|
进价(元/台) |
1800 |
1500 |
|
售价(元/台) |
2000 |
1600 |
计划购进电视机和洗衣机共100台,商店最多可筹集资金161 800元.
(1)请你帮助商店算一算有多少种进货方案?(不考虑除进价之外的其它费用)
(2)哪种进货方案待商店销售购进的电视机与洗衣机完毕后获得利润最多?并求出最多利润.(利润=售价-进价)
解:(1)设商店购进电视机x台,则购进洗衣机(100-x)台,根据题意,得
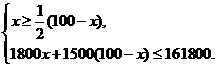 ,解不等式组,得
,解不等式组,得 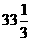 ≤x≤
≤x≤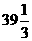 .
即购进电视机最少34台,最多39台,商店有6种进货方案.
(2)设商店销售完毕后获利为y元,根据题意,得
y=(2000-1800)x+(1600-1500)(100-x)=100x+10000.
∵ 100>0,∴ 当x最大时,y的值最大.
即 当x=39时,商店获利最多为13900元.
.
即购进电视机最少34台,最多39台,商店有6种进货方案.
(2)设商店销售完毕后获利为y元,根据题意,得
y=(2000-1800)x+(1600-1500)(100-x)=100x+10000.
∵ 100>0,∴ 当x最大时,y的值最大.
即 当x=39时,商店获利最多为13900元.
10、(2007重庆)我市某镇组织20辆汽车装运完A、B、C三种脐橙共100吨到外地销售。按计划,20辆汽车都要装运,每辆汽车只能装运同一种脐橙,且必须装满。根据下表提供的信息,解答以下问题:
|
脐 橙 品 种 |
A |
B |
C |
|
每辆汽车运载量(吨) |
6 |
5 |
4 |
|
每吨脐橙获得(百元) |
12 |
16 |
10 |
(1)设装运A种脐橙的车辆数为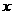 ,装运B种脐橙的车辆数为
,装运B种脐橙的车辆数为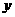 ,求
,求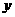 与
与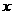 之间的函数关系式;
之间的函数关系式;
(2)如果装运每种脐橙的车辆数都不少于4辆,那么车辆的安排方案有几种?并写出每种安排方案;
(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值。
解:(1)根据题意,装运A种脐橙的车辆数为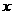 ,装运B种脐橙的车辆数为
,装运B种脐橙的车辆数为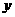 ,那么装运C种脐橙的车辆数为
,那么装运C种脐橙的车辆数为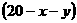 ,则有:
,则有:
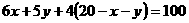 整理得:
整理得: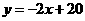
(2)由(1)知,装运A、B、C三种脐橙的车辆数分别为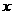 、
、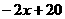 、
、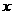 ,由题意得:
,由题意得: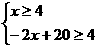 ,解得:4≤
,解得:4≤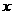 ≤8,因为
≤8,因为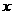 为整数,所以
为整数,所以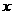 的值为4、5、6、7、8,所以安排方案共有5种。
的值为4、5、6、7、8,所以安排方案共有5种。
方案一:装运A种脐橙4车,B种脐橙12车,C种脐橙4车;
方案二:装运A种脐橙5车,B种脐橙10车,C种脐橙5车;
方案三:装运A种脐橙6车,B种脐橙8车,C种脐橙6车;
方案四:装运A种脐橙7车,B种脐橙6车,C种脐橙7车;
方案五:装运A种脐橙8车,B种脐橙4车,C种脐橙8车;
(3)设利润为W(百元)则:
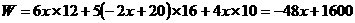
∵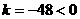 ∴W的值随
∴W的值随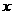 的增大而减小
的增大而减小
要使利润W最大,则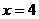 ,故选方案一
,故选方案一
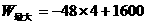 =1408(百元)=14.08(万元)
=1408(百元)=14.08(万元)
答:当装运A种脐橙4车,B种脐橙12车,C种脐橙4车时,获利最大,最大利润为14.08万元。
9、(2007山东青岛)某饮料厂开发了A、B两种新型饮料,主要原料均为甲和乙,每瓶饮料中甲、乙的含量如下表所示.现用甲原料和乙原料各2800克进行试生产,计划生产A、B两种饮料共100瓶.设生产A种饮料x瓶,解答下列问题:
(1)有几种符合题意的生产方案?写出解答过程;
(2)如果A种饮料每瓶的成本为2.60元,B种饮料每瓶的成本为2.80元,这两种饮料成本总额为y元,请写出y与x之间的关系式,并说明x取何值会使成本总额最低?
|
原料名称 饮料名称 |
甲 |
乙 |
|
A |
20克 |
40克 |
|
B |
30克 |
20克 |
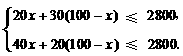 解:⑴ 设生产A种饮料x瓶,根据题意得:
解:⑴ 设生产A种饮料x瓶,根据题意得:
解这个不等式组,得20≤x≤40.
因为其中正整数解共有21个,
所以符合题意的生产方案有21种.
⑵ 根据题意,得 y=2.6x+2.8(100-x).
整理,得 y=-0.2x+280.
∵k=-0.2<0,
∴y随x的增大而减小.
∴当x=40时成本总额最低.
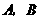 两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个
两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个 种造型需甲种花卉80盆,乙种花卉40盆,搭配一个
种造型需甲种花卉80盆,乙种花卉40盆,搭配一个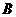 种造型需甲种花卉50盆,乙种花卉90盆.
种造型需甲种花卉50盆,乙种花卉90盆.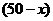 个,
个,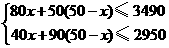
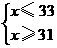 ,
,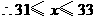
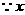 是整数,
是整数,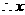 可取
可取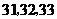 ,
, 可设计三种搭配方案:
可设计三种搭配方案: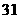 个
个 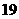 个
个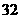 个
个 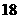 个
个 个
个 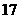 个.
个. 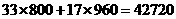 (元)
(元)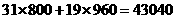 (元)
(元)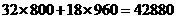 (元)
(元)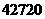 元
元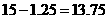 (km)
(km)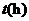 后先步行的4人相遇,
后先步行的4人相遇,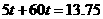 ,解得
,解得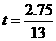 .
.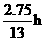 .······················································· 9分
.······················································· 9分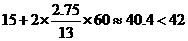 .
. 的
的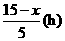 ,
,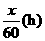 先步行的4人走了
先步行的4人走了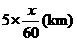 ,
,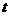 (h)后与先步行的4人相遇,则有
(h)后与先步行的4人相遇,则有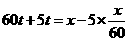 ,解得
,解得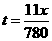 ,
,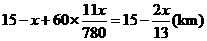 .
.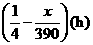 .
.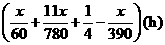 ,
,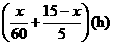 ,
,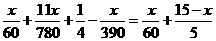 ,解得
,解得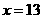 .
.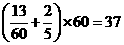 (分钟).
(分钟).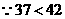 .
.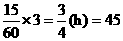 (分钟),
(分钟),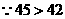 ,
,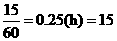 (分钟).
(分钟). (2)如果小区投资46.9万元,问能否完成工程任务,若能,请写出x为整数的所有工程方案;若不能,请说明理由。(参考值:
(2)如果小区投资46.9万元,问能否完成工程任务,若能,请写出x为整数的所有工程方案;若不能,请说明理由。(参考值: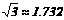 )
)
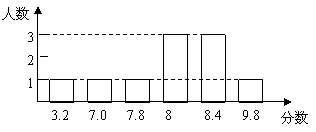

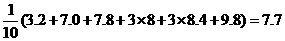 ;··············· 1分
;··············· 1分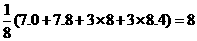 ;····················································· 2分
;····················································· 2分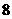 ;··································································································· 3分
;··································································································· 3分 .························································································· 4分
.························································································· 4分