(二)若将(一)中所做实验用的“正四面体骰子”改为“各
面标有1 至6这六个数字中的一个的正方体骰子”,其余(实验
|
出点P落在正方形ABCD面上的概率.
[解](一)(1) 根据题意,点P的横坐标有数字1,2,3,4四种选择,点P的纵坐标也有数字1,2,3,4四种选择,所以构成点P的坐标共有4×4 = 16种情况.其中点P的(1,1),(1,2),(2,1),(2,2)四种情况将落在正方形ABCD面上,故所求的概率为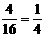 .
.
(2)因为要使点P落在正方形ABCD面上的概率为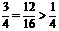 ,所以只能将正方
,所以只能将正方
形ABCD向上或向右整数个单位平移,且使点P落在正方形面上的数目为12.存
在满足题设要求的平移方式:先将正方形ABCD上移2个单位,后右移1个单位
(先右后上亦可);或先将正方形ABCD上移1个单位,后右移2个单位(先右后
上亦可).
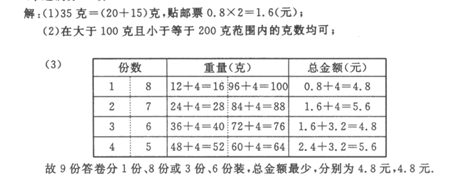
2 4.今年,苏州市政府的一项实事工程就是由政府投人1 000万元资金.对城区4万户家庭的老式水龙头和13升抽水马桶进行免费改造.某社区为配合政府完成该项工作,对社区内1200户家庭中的120户进行了随机抽样调查,并汇总成下表:
4.今年,苏州市政府的一项实事工程就是由政府投人1 000万元资金.对城区4万户家庭的老式水龙头和13升抽水马桶进行免费改造.某社区为配合政府完成该项工作,对社区内1200户家庭中的120户进行了随机抽样调查,并汇总成下表:
|
改造 情况 |
均不 改造 |
改造水龙头 |
改造马桶 |
||||
|
1个 |
2个 |
3个 |
4个 |
1个 |
2个 |
||
|
户数 |
20 |
31 |
28 |
21 |
12 |
69 |
2 |
(1)试估计该社区需要对水龙头、马桶进行改造的家庭共有_____户;
(2)改造后.一只水龙头一年大约可节省5吨水,一只马桶一年大约可节省15吨水.试估
计该社区一年共可节约多少吨自来水?
(3)在抽样的120户家庭中.既要改造水龙头又要改造马桶的家庭共有多少户?
解:(1) 1000;
(2) 抽样的120户家庭一年共可节约用水:
(1×31+2×28+×21+4×12)× 5+(1×69+2×2)×15=198×5+73×15=2085。
2085×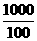 =20850(吨)。
=20850(吨)。
答:该社区一年共可节约用水20850吨。
(3) 设既要改造水龙头又要改造马桶的家庭共有x户,则只改造水龙头不改造马桶的家庭共有(92-x)户,只改造马桶不改造水龙头的家庭共有(71-x)户,
∴ x+(92-x)+(71一x)=100,
∴x=63(户)。
答:既要改造水龙头又要改造马桶的家庭共有63户.
25.(一)如图,放在直角坐标系中的正方形ABCD的边长为4.现做如下实验:
 抛掷一枚均匀的正四面体骰子(它有四个顶点,各顶点的点数分别是1至4这四个数字中的一个),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的顶点的点数作为直角坐标系中P点的坐标(第一次的点数作横坐标,第二次的点数作纵坐标).
抛掷一枚均匀的正四面体骰子(它有四个顶点,各顶点的点数分别是1至4这四个数字中的一个),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的顶点的点数作为直角坐标系中P点的坐标(第一次的点数作横坐标,第二次的点数作纵坐标).
(1)求P点落在正方形ABCD面上(含正方形内和边界,下同)
的概率;
(2)将正方形ABCD平移整数个单位,则是否存在一种平移,
 使点P落在正方形ABCD面上的概率为
使点P落在正方形ABCD面上的概率为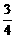 ?若存在,指出其中
?若存在,指出其中
的一种平移方式;若不存在,请说明理由.
 小明把自己一周的支出情况,用右图所示的统计图来表示,下面说法正确的是 ( )
小明把自己一周的支出情况,用右图所示的统计图来表示,下面说法正确的是 ( )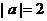 ,
,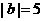 .求
.求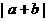 的值为7的概率.
的值为7的概率.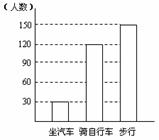 (A)0.12 (B)0.38
(C)0.32 (D)3.12
(A)0.12 (B)0.38
(C)0.32 (D)3.12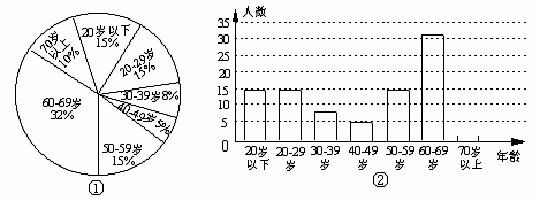 例11:在市政府举办的“迎奥运登山活动”中,参加白云山景区登山活动的市民约有12000人,为统计参加活动人员的年龄情况,我们从中随机抽取了100人的年龄作为样本,进行数据处理,制成扇形统计图和条形统计图(部分)如下:
例11:在市政府举办的“迎奥运登山活动”中,参加白云山景区登山活动的市民约有12000人,为统计参加活动人员的年龄情况,我们从中随机抽取了100人的年龄作为样本,进行数据处理,制成扇形统计图和条形统计图(部分)如下: 例7:甲、乙两人各射靶5次,已知甲所中环数是8、7、9、7、9,乙所中的环数的平均数x=8,方差S2乙=0.4,那么,对甲、乙的射击成绩的正确判断是( )
例7:甲、乙两人各射靶5次,已知甲所中环数是8、7、9、7、9,乙所中的环数的平均数x=8,方差S2乙=0.4,那么,对甲、乙的射击成绩的正确判断是( ) .
. ,
,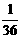 ,即
,即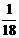 ,
,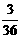 ,
,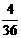 ,
,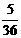 ,即
,即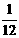 ,
,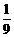 ,
,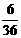 ,
,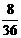 ,
,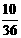 ,即
,即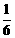 ,
,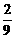 ,
,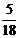 .
.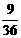 ,
,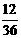 ,
,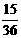 ,即
,即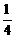 ,
,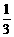 ,
,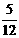 .
.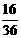 ,
,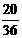 ,即
,即 ,
, .
. ,即
,即 .
.