7.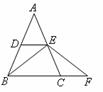 如图5,在
如图5,在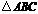 中,
中,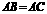 ,点
,点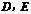 分别是
分别是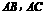 的中点,
的中点,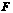 是
是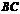 延长线上的一点,且
延长线上的一点,且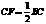 .
.
(1)求证: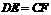 ;
;
|
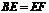 .
.
证明:(1)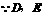 分别为
分别为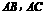 的中点,
的中点,
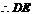 为中位线.
为中位线.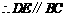 ,且
,且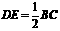 ;
;
又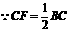 ,
,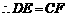 .
.
(2)连结 .由(1)可得
.由(1)可得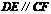 ,且
,且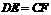 ,
,
 四边形
四边形 为平行四边形,
为平行四边形,
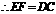 .
.
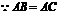 ,且
,且 为中位线,
为中位线, 四边形
四边形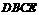 为等腰梯形,
为等腰梯形,
又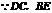 为等腰梯形
为等腰梯形 的对角线,
的对角线,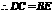 ,
,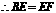 .
.
6.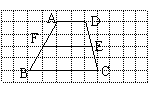 如图,梯形ABCD在边长为1的小正方形网格中位置如图所示,EF为中位线,则S梯形ADEF:S梯形EFBC=( )
如图,梯形ABCD在边长为1的小正方形网格中位置如图所示,EF为中位线,则S梯形ADEF:S梯形EFBC=( )
A 2:5
B.11:17
C C.1:2
|
核心能力-----技能关
4.如图,在梯形ABCD中,AB//CD,中位线EF与对角线AC、BD交于M、N两点,若EF=18cm,MN=8cm,则AB的长等于( A )
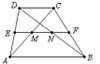 A.10cm B.13cm
A.10cm B.13cm
C.20cm D.26cm
|
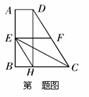
3.如图:在直角梯形 中,
中,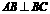 ,
,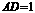 ,
,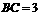 ,
, ,
,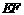 为梯形的中位线,
为梯形的中位线, 为梯形的高,则下列结论:①
为梯形的高,则下列结论:①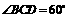 ,②四边形
,②四边形 为菱形,③
为菱形,③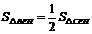 ,④以
,④以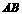 为直径的圆与
为直径的圆与 相切于点
相切于点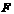 ,其中正确结论的个数为( B ).
,其中正确结论的个数为( B ).
 A.4 B.3
A.4 B.3
|
11、如图,某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品,下表是活动进行中的一组统计数据:
⑴ 计算并完成表格;
转动转盘的次数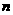 |
100 |
150 |
200 |
500 |
800 |
1000 |
落在“铅笔”的次数 |
68 |
111 |
136 |
345 |
564 |
701 |
落在“铅笔”的频率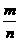 |
|
|
|
|
|
|
⑵ 请估计当n很大时,频率将会接近多少?
⑶
 假如你去转动该转盘一次,你获得可乐的概率是多少?在该转盘中,表示“可乐”区域的扇形的圆心角约是多少度?
假如你去转动该转盘一次,你获得可乐的概率是多少?在该转盘中,表示“可乐”区域的扇形的圆心角约是多少度?
⑷ 如果转盘被一位小朋友不小心损坏,
请你设计一个等效的模拟实验方案(要求
交代清楚替代工具和游戏规则).
 ),在直角梯形
),在直角梯形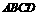 ,
,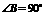 ,
,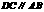 ,动点
,动点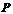 从
从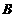 点出发,由
点出发,由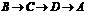 沿边运动,设点
沿边运动,设点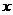 ,
, 的面积为
的面积为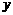 ,如果关于
,如果关于 的函数
的函数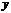 的图象如图2(
的图象如图2(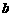 ),则
),则 的面积为( B )
的面积为( B )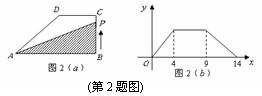
 中,
中,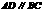 ,对角线
,对角线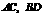 相交于点
相交于点 ,有如下四个 结论:①
,有如下四个 结论:①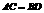 ;②
;②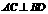 ;③等腰梯形
;③等腰梯形 是中心对称图形;④
是中心对称图形;④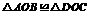 .则正确的结论是( )
.则正确的结论是( )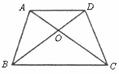 A.①④
A.①④ 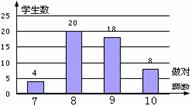 A、8, 8 B、8,9
A、8, 8 B、8,9