17、(2007哈尔滨)青青商场经销甲、乙两种商品,甲种商品每件进价15元,售价20元;乙种商品每件进价35元,售价45元.
(1)若该商场同时购进甲、乙两种商品共100件恰好用去2700元,求能购进甲、乙两种商品各多少件?
(2)该商场为使甲、乙两种商品共100件的总利润(利润=售价 进价)不少于750元,且不超过760元,请你帮助该商场设计相应的进货方案;
进价)不少于750元,且不超过760元,请你帮助该商场设计相应的进货方案;
(3)在“五·一”黄金周期间,该商场对甲、乙两种商品进行如下优惠促销活动:
|
打折前一次性购物总金额 |
优惠措施 |
|
不超过300元 |
不优惠 |
|
超过300元且不超过400元 |
售价打九折 |
|
超过400元 |
售价打八折 |
按上述优惠条件,若小王第一天只购买甲种商品一次性付款200元,第二天只购买乙种商品打折后一次性付款324元,那么这两天他在该商场购买甲、乙两种商品一共多少件?(通过计算求出所有符合要求的结果)
解:(1)设该商场能购进甲种商品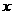 件,根据题意,得
件,根据题意,得
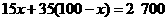 ··························································································· 1分
··························································································· 1分
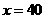
乙种商品: (件)··················································································· 1分
(件)··················································································· 1分
答:该商品能购进甲种商品40件,乙种商品60件.
(2)设该商场购进甲种商品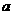 件,则购进乙种商品
件,则购进乙种商品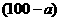 件.根据题意,得
件.根据题意,得
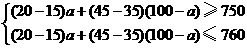 ······································································· 1分
······································································· 1分
因此,不等式组的解集为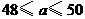 ········································································· 1分
········································································· 1分
根据题意,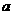 的值应是整数,
的值应是整数,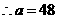 或
或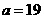 或
或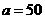
 该商场共有三种进货方案:
该商场共有三种进货方案:
方案一:购进甲种商品48件,乙种商品52件,
方案二:购进甲种商品49件,乙种商品51件,
方案三:购进甲种商品50件,乙种商品50件.···························································· 1分
(3)根据题意,得
第一天只购买甲种商品不享受优惠条件 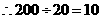 (件)·································· 1分
(件)·································· 1分
第二天只购买乙种商品有以下两种情况:
情况一:购买乙种商品打九折,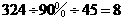 (件)
(件)
情况二:购买乙种商品打八折,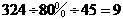 (件)
(件)
 一共可购买甲、乙两种商品
一共可购买甲、乙两种商品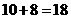 (件)··························································· 1分
(件)··························································· 1分
或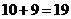 (件)····································································································· 1分
(件)····································································································· 1分
答:这两天他在该商场购买甲、乙两种商品一共18件或19件.
15、(2007四川绵阳)绵阳市“全国文明村”江油白玉村果农王灿收获枇杷20吨,桃子12吨.现计划租用甲、乙两种货车共8辆将这批水果全部运往外地销售,已知一辆甲种货车可装枇杷4吨和桃子1吨,一辆乙种货车可装枇杷和桃子各2吨.
(1)王灿如何安排甲、乙两种货车可一次性地运到销售地?有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果农王灿应选择哪种方案,使运输费最少?最少运费是多少?
解:(1)设安排甲种货车x辆,则安排乙种货车(8-x)辆,依题意,得
4x + 2(8-x)≥20,且x + 2(8-x)≥12,
解此不等式组,得 x≥2,且 x≤4, 即 2≤x≤4.
∵ x是正整数, ∴ x可取的值为2,3,4.
因此安排甲、乙两种货车有三种方案:
|
|
甲种货车 |
乙种货车 |
|
方案一 |
2辆 |
6辆 |
|
方案二 |
3辆 |
5辆 |
|
方案三 |
4辆 |
4辆 |
(2)方案一所需运费 300×2 + 240×6 = 2040元;
方案二所需运费 300×3 + 240×5 = 2100元;
方案三所需运费 300×4 + 240×4 = 2160元.
所以王灿应选择方案一运费最少,最少运费是2040元.
 的绝对值是
的绝对值是 辆··········································· 1分
辆··········································· 1分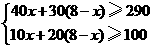 ·············································································· 4分
·············································································· 4分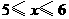 ········································································································· 5分
········································································································· 5分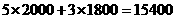 元;
元;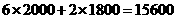 元··············································· 7分
元··············································· 7分