29.(本题满分10分)
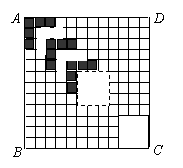 如图,正方形ABCD的边长为12,划分成12×12个
如图,正方形ABCD的边长为12,划分成12×12个
小正方形. 将边长为n(n为整数,且2≤n≤11)的黑白
两色正方形纸片按图中的方式黑白相间地摆放,第一张
n×n的纸片正好盖住正方形ABCD左上角的n×n个小正
方形格,第二张纸片盖住第一张纸片的部分恰好为(n-1)
×(n-1)的正方形. 如此摆放下去,最后直到纸片盖住
正方形ABCD的右下角为止. 请你认真观察思考后回答下
列问题:
(1)由于正方形纸片边长n的取值不同,完成摆放时所使用正方形纸 片的张数也不同,请填写下表:
|
纸片的边长n |
2 |
3 |
4 |
5 |
6 |
|
使用的纸片张数 |
|
|
|
|
|
(2)设正方形ABCD被纸片盖住的面积(重合部分只计一次)为S1,未被盖住的面积为S2.
①当n=2时,求S1∶S2的值;
②是否存在使得S1=S2的n值?若存在,请求出这样的n值;若不存在,请说明理由.
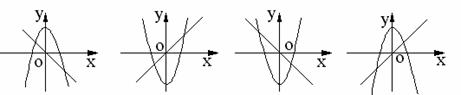 在直角坐标系中,函数y= -3x与y=x2-1的图象大致是( )
在直角坐标系中,函数y= -3x与y=x2-1的图象大致是( )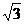 cm
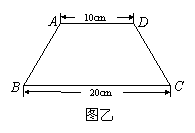
cm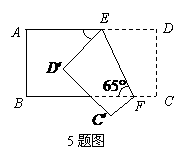 如图,把一个长方形纸片沿EF折叠后,点D、C分别落在
如图,把一个长方形纸片沿EF折叠后,点D、C分别落在 、
、 的位置,若
的位置,若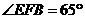 ,则
,则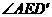 等于( )
等于( )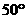 B、
B、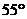 C、
C、 D、
D、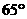
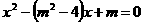 的两个实根互为相反数,则
的两个实根互为相反数,则 的值是( )
的值是( )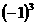 和1
B、
和1
B、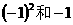 C、
C、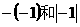 D、
D、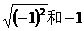
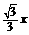 ,关于x的一元二次方程
,关于x的一元二次方程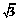 -1,试判断ΔOBC的形状;
-1,试判断ΔOBC的形状;