32.(辽宁卷)现有甲、乙两个项目,对甲项目每投资十万元,一年后利润是1.2万元、1.18万元、1.17万元的概率分别为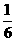 、
、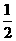 、
、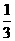 ;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是
;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是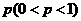 ,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为
,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为 ,对乙项目每投资十万元,
,对乙项目每投资十万元,  取0、1、2时,
一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量
取0、1、2时,
一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量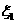 、
、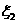 分别表示对甲、乙两项目各投资十万元一年后的利润.
分别表示对甲、乙两项目各投资十万元一年后的利润.
(I) 求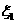 、
、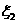 的概率分布和数学期望
的概率分布和数学期望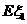 、
、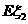 ;
;
(II) 当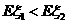 时,求
时,求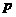 的取值范围.
的取值范围.
[解析](I)解法1:
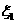 的概率分布为
的概率分布为
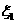 |
1.2 |
1.18 |
1.17 |
|
P |
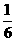 |
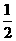 |
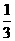 |
E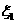 =1.2
=1.2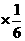 +1.18
+1.18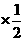 +1.17
+1.17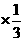 =1.18.
=1.18.
由题设得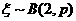 ,则
,则 的概率分布为
的概率分布为
 |
0 |
1 |
2 |
|
P |
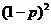 |
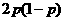 |
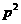 |
故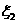 的概率分布为
的概率分布为
 |
1.3 |
1.25 |
0.2 |
|
P |
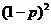 |
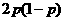 |
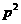 |
所以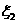 的数学期望为
的数学期望为
E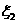 =
=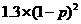 +
+ +
+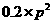 =
=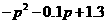 .
.
解法2: 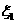 的概率分布为
的概率分布为
 |
1.2 |
1.18 |
1.17 |
|
P |
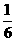 |
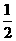 |
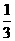 |
E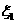 =1.2
=1.2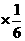 +1.18
+1.18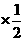 +1.17
+1.17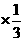 =1.18.
=1.18.
设 表示事件”第i次调整,价格下降”(i=1,2),则
表示事件”第i次调整,价格下降”(i=1,2),则
P( =0)=
=0)= 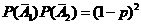 ;
;
P( =1)=
=1)=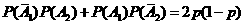 ;
;
P( =2)=
=2)=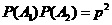
故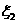 的概率分布为
的概率分布为
 |
1.3 |
1.25 |
0.2 |
|
P |
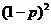 |
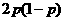 |
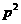 |
所以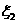 的数学期望为
的数学期望为
E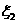 =
=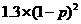 +
+ +
+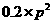 =
=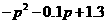 .
.
(II) 由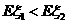 ,得:
,得:
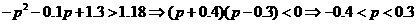
因0<p<1,所以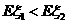 时,p的取值范围是0<p<0.3.
时,p的取值范围是0<p<0.3.
[点评]本小题考查二项分布、分布列、数学期望、方差等基础知识,考查同学们运用概率知识解决实际问题的能力.
30.(江西卷)某商场举行抽奖促销活动,抽奖规则是:从装有9个白球,1个红球的箱子中每次随机地摸出一个球,记下颜色后放回,摸出一个红球可获得奖金10元;摸出2个红球可获得奖金50元,现有甲,乙两位顾客,规定:甲摸一次,乙摸两次,令x表示甲,乙摸球后获得的奖金总额。求:
(1)x的分布列
(2)x的的数学期望
解:(1) 的所有可能的取值为0,10,20,50,60.
的所有可能的取值为0,10,20,50,60.
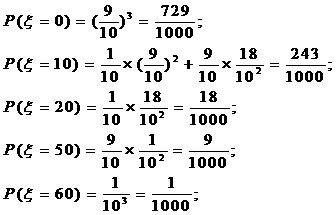
分布列为
|
x |
0 |
10 |
20 |
50 |
60 |
|
P |
  |
 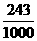 |
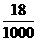 |
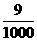 |
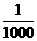 |
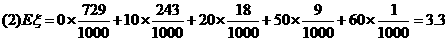 (元)
(元)
27.(湖北卷)在某校举行的数学竞赛中,全体参赛学生的竞赛成绩近似服从正态分布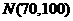 。已知成绩在90分以上(含90分)的学生有12名。
。已知成绩在90分以上(含90分)的学生有12名。
(Ⅰ)、试问此次参赛学生总数约为多少人?
(Ⅱ)、若该校计划奖励竞赛成绩排在前50名的学生,试问设奖的分数线约为多少分?
可共查阅的(部分)标准正态分布表
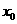 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1.2 1.3 1.4 1.9 2.0 2.1 |
0.8849 0.9032 0.9192 0.9713 0.9772 0.9821 |
0.8869 0.9049 0.9207 0.9719 0.9778 0.9826 |
0.888 0.9066 0.9222 0.9726 0.9783 0.9830 |
0.8907 0.9082 0.9236 0.9732 0.9788 0.9834 |
0.8925 0.9099 0.9251 0.9738 0.9793 0.9838 |
0.8944 0.9115 0.9265 0.9744 0.9798 0.9842 |
0.8962 0.9131 0.9278 0.9750 0.9803 0.9846 |
0.8980 0.9147 0.9292 0.9756 0.9808 0.9850 |
0.8997 0.9162 0.9306 0.9762 0.9812 0.9854 |
0.9015 0.9177 0.9319 0.9767 0.9817 0.9857 |
点评:本小题主要考查正态分布,对独立事件的概念和标准正态分布的查阅,考查运用概率统计知识解决实际问题的能力。
解:(Ⅰ)设参赛学生的分数为 ,因为
,因为 -N(70,100),由条件知,
-N(70,100),由条件知,
P( ≥90)=1-P(
≥90)=1-P( <90)=1-F(90)=1-
<90)=1-F(90)=1-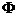
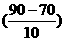 =1-
=1-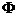 (2)=1-0.9772=0.228.
(2)=1-0.9772=0.228.
这说明成绩在90分以上(含90分)的学生人数约占全体参赛人数的2.28%,因此,
参赛总人数约为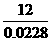 ≈526(人)。
≈526(人)。
(Ⅱ)假定设奖的分数线为x分,则P( ≥x)=1-P(
≥x)=1-P( <x)=1-F(90)=1-
<x)=1-F(90)=1-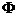
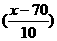 =
=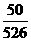 =0.0951,即
=0.0951,即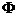
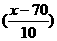 =0.9049,查表得
=0.9049,查表得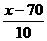 ≈1.31,解得x=83.1.
≈1.31,解得x=83.1.
故设奖得分数线约为83.1分。
26.(广东卷)某运动员射击一次所得环数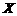 的分布如下:
的分布如下:
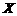 |
6 |
7 |
8 |
9 |
10 |
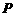 |
0 |
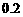 |
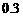 |
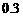 |
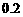 |
现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为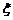 .
.
(I)求该运动员两次都命中7环的概率
(II)求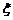 的分布列
的分布列
解:(Ⅰ)求该运动员两次都命中7环的概率为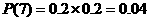 ;
;
(Ⅱ)
 的可能取值为7、8、9、10
的可能取值为7、8、9、10
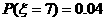

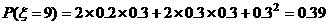
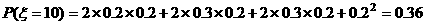
 分布列为
分布列为
 |
7 |
8 |
9 |
10 |
|
P |
0.04 |
0.21 |
0.39 |
0.36 |
(Ⅲ)  的数学希望为
的数学希望为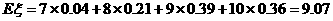 .
.
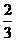 ,服用B有效的概率为
,服用B有效的概率为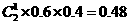
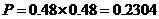
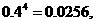
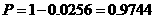
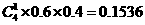
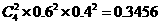
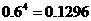
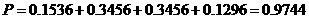
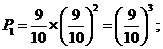
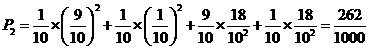
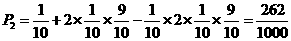
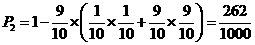
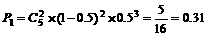 .
.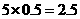 ,即平均有2.50家煤矿必须整改.
,即平均有2.50家煤矿必须整改.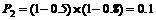 ,从而该煤矿不被关闭的概率是0.9.由题意,每家煤矿是否被关闭是相互独立的,所以至少关闭一家煤矿的概率是
,从而该煤矿不被关闭的概率是0.9.由题意,每家煤矿是否被关闭是相互独立的,所以至少关闭一家煤矿的概率是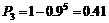
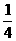 ,且该组中,青年人占50%,中年人占40%,老年人占10%。为了了解各组不同的年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本。试确定
,且该组中,青年人占50%,中年人占40%,老年人占10%。为了了解各组不同的年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本。试确定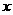 ,游泳组中,青年人、中年人、老年人各占比例分别为a、b、c,则有
,游泳组中,青年人、中年人、老年人各占比例分别为a、b、c,则有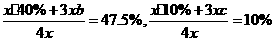 ,解得b=50%,c=10%.
,解得b=50%,c=10%.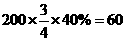 (人);抽取的中年人数为
(人);抽取的中年人数为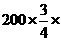 50%=75(人);抽取的老年人数为
50%=75(人);抽取的老年人数为