0 446819 446827 446833 446837 446843 446845 446849 446855 446857 446863 446869 446873 446875 446879 446885 446887 446893 446897 446899 446903 446905 446909 446911 446913 446914 446915 446917 446918 446919 446921 446923 446927 446929 446933 446935 446939 446945 446947 446953 446957 446959 446963 446969 446975 446977 446983 446987 446989 446995 446999 447005 447013 447348
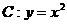 的焦点为F,动点P在直线
的焦点为F,动点P在直线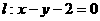 上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点.
上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点. ,
,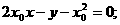
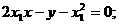
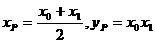
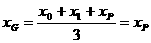 ,
,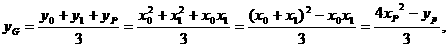
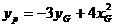 ,由点P在直线l上运动,从而得到重心G的轨迹方程为:
,由点P在直线l上运动,从而得到重心G的轨迹方程为: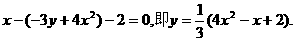
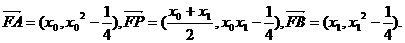
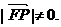

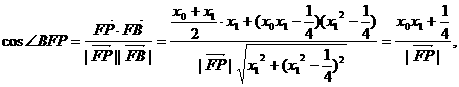
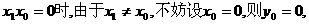 所以P点坐标为
所以P点坐标为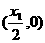 ,则P点到直线AF的距离为:
,则P点到直线AF的距离为:
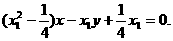
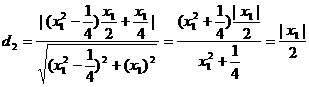
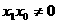 时,直线AF的方程:
时,直线AF的方程:
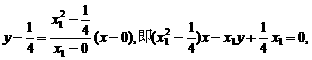
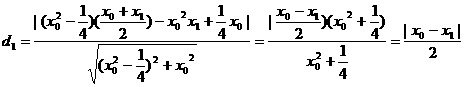 ,同理可得到P点到直线BF的距离
,同理可得到P点到直线BF的距离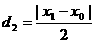 ,因此由d1=d2,可得到∠AFP=∠PFB.
,因此由d1=d2,可得到∠AFP=∠PFB.
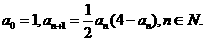

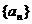 的通项公式an.
的通项公式an.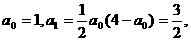
 ,命题正确.
,命题正确.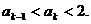
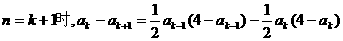


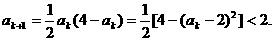
 时命题正确.
时命题正确.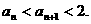
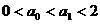 ;
;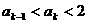 成立,
成立,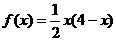 ,
,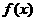 在[0,2]上单调递增,所以由假设
在[0,2]上单调递增,所以由假设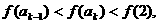 即
即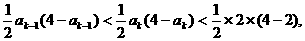
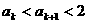 成立,所以对一切
成立,所以对一切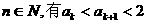
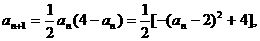 所以
所以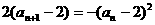
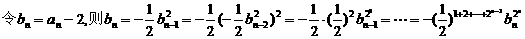 ,
, .
.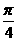 .
.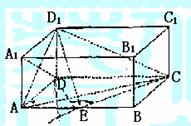
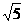 ,AD1=
,AD1=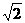 ,
,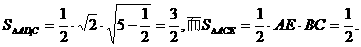
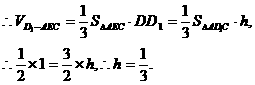


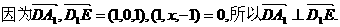
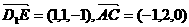 ,
, ,设平面ACD1的法向量为
,设平面ACD1的法向量为 ,则
,则
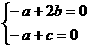 ,得
,得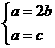 ,从而
,从而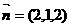 ,所以点E到平面AD1C的距离为
,所以点E到平面AD1C的距离为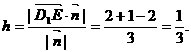

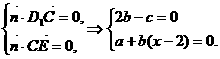 令b=1,
∴c=2,a=2-x,
令b=1,
∴c=2,a=2-x,
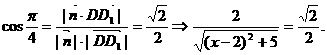
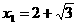 (不合,舍去),
(不合,舍去),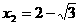 .
.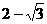 时,二面角D1-EC-D的大小为
时,二面角D1-EC-D的大小为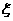 表示游戏终止时掷硬币的次数.
表示游戏终止时掷硬币的次数. ,
,


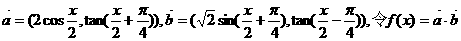 .
. 若存在,则求出x的值;若不存在,则证明之.
若存在,则求出x的值;若不存在,则证明之.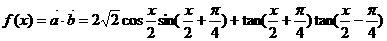


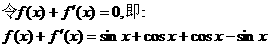


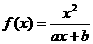 (a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3,
x2=4.
(a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3,
x2=4.
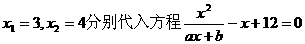 得
得

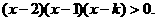
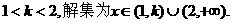
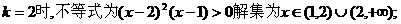
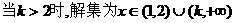 .
.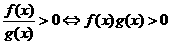 ,
,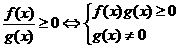
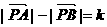 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;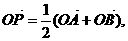 则动点P的轨迹为椭圆;
则动点P的轨迹为椭圆;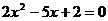 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率; 有相同的焦点.
有相同的焦点. ,那么P点的轨迹为双曲线,故①错,
,那么P点的轨迹为双曲线,故①错,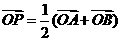 ,得P为弦AB的中点,故②错,
,得P为弦AB的中点,故②错, 的两根为
的两根为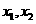 则
则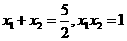 可知两根互与为倒数,且均为正,故③对,
可知两根互与为倒数,且均为正,故③对,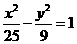 的焦点坐标(
的焦点坐标(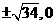 ),而
),而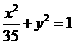 的焦点坐标(
的焦点坐标(
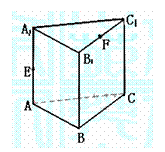 如图,在直三棱柱ABC-A1B1C1中,
如图,在直三棱柱ABC-A1B1C1中, ,
,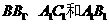 将E、F展开到同一平面内,则易得:
将E、F展开到同一平面内,则易得: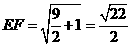 ,
,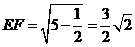 ,或
,或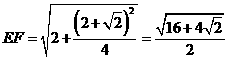
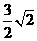 .
. 设实数x,
y满足
设实数x,
y满足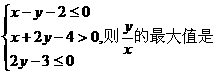 .
.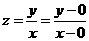 表示两点(0,0),A(x,y)的斜率
表示两点(0,0),A(x,y)的斜率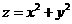 的几何意义吗?
的几何意义吗?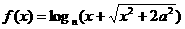 是奇函数,则a=
.
是奇函数,则a=
.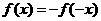 ,即
,即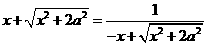 ,
,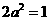 ,
,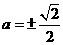 .
.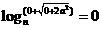 ,得
,得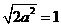 即
即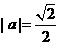 推出答案
推出答案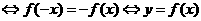 的图象关于原点对称.
的图象关于原点对称. 的图象关于y轴对称.
的图象关于y轴对称.