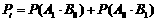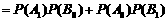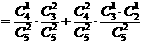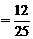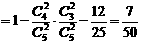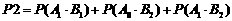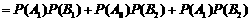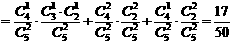38.(山东卷)袋中装着标有数学1,2,3,4,5的小球各2个,从袋中任取3个小球,按3个小球上最大数字的9倍计分,每个小球被取出的可能性都相等,用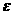 表示取出的3个小球上的最大数字,求:
(1)取出的3个小球上的数字互不相同的概率;
表示取出的3个小球上的最大数字,求:
(1)取出的3个小球上的数字互不相同的概率;
(2)随机变量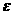 的概率分布和数学期望;
的概率分布和数学期望;
(3)计分介于20分到40分之间的概率.
解:(I)解法一:“一次取出的3个小球上的数字互不相同”的事件记为 ,
,
则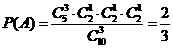
解法二:“一次取出的3个小球上的数字互不相同的事件记为A”,“一次取出的3个小球上有两个数字相同”的事件记为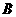 ,则事件
,则事件 和事件
和事件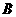 是互斥事件,因为
是互斥事件,因为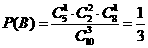 ,所以
,所以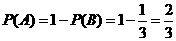 .
.
(II)由题意 有可能的取值为:2,3,4,5.
有可能的取值为:2,3,4,5.
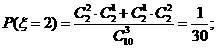
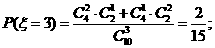
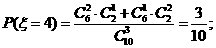
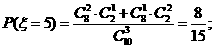
所以随机变量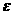 的概率分布为
的概率分布为
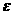 |
2 |
3 |
4 |
5 |
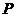 |
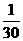 |
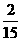 |
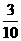 |
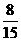 |
因此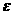 的数学期望为
的数学期望为
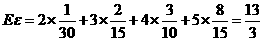
(Ⅲ)“一次取球所得计分介于20分到40分之间”的事件记为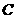 ,则
,则

36.(全国II)某批产品成箱包装,每箱5件.一用户在购进该批产品前先取出3箱,再从每箱中任意抽取2件产品进行检验.设取出的第一、二、三箱中分别有0件、1件、2件二等品,其余为一等品.
(Ⅰ)用ξ表示抽检的6件产品中二等品的件数,求ξ的分布列及ξ的数学期望;
(Ⅱ)若抽检的6件产品中有2件或2件以上二等品,用户就拒绝购买这批产品,求这批产品级用户拒绝的概率.
解(1.) 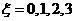
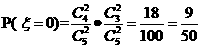
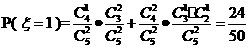
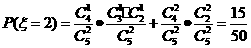
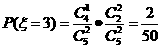
所以 的分布列为
的分布列为
 |
0 |
1 |
2 |
3 |
|
P |
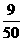 |
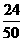 |
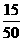 |
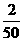 |
 的数学期望E(
的数学期望E( )=
)=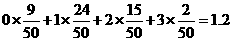
(2)P(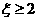 )=
)=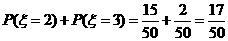
本题主要考察分布列的求法以及利用分布列求期望和概率,难度对于民族地区学生较大
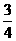 ,求n.
,求n.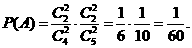
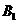 ,“取到的4个球全是白球”为事件
,“取到的4个球全是白球”为事件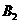 .由题意,得
.由题意,得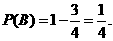
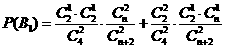
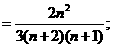

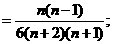
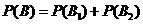
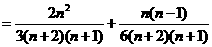
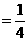 ,
,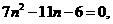
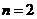 ,或
,或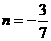 (舍去),
(舍去),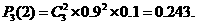
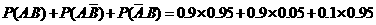
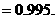
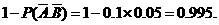
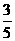 ,且各次射击的结果互不影响。
,且各次射击的结果互不影响。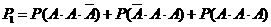
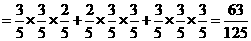
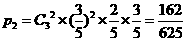
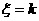 ”的概率为
”的概率为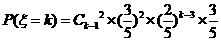
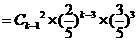 (
(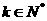 且
且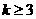 )
)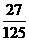
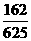
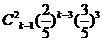
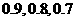 ;在实验考核中合格的概率分别为
;在实验考核中合格的概率分别为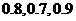 ,所有考核是否合格相互之间没有影响
,所有考核是否合格相互之间没有影响 ;“乙理论考核合格”为事件
;“乙理论考核合格”为事件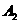 ;“丙理论考核合格”为事件
;“丙理论考核合格”为事件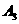 ;记
;记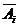 为
为 的对立事件,
的对立事件,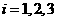 ;记“甲实验考核合格”为事件
;记“甲实验考核合格”为事件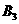 ;
;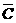 为
为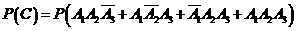
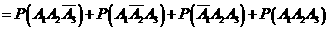
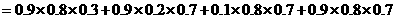
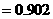
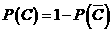
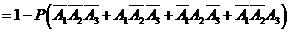
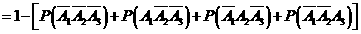
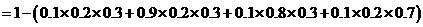
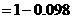
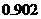
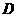
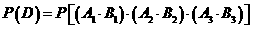
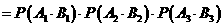
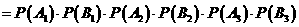
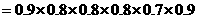
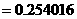
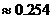
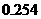
 .
.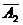 .
. )=P(
)=P(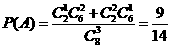
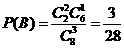
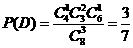
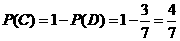 .
. 表示事件“第二箱中取出i件二等品”,i=0,1;
表示事件“第二箱中取出i件二等品”,i=0,1; 表示事件“第三箱中取出i件二等品”,i=0,1,2;
表示事件“第三箱中取出i件二等品”,i=0,1,2;