0 446803 446811 446817 446821 446827 446829 446833 446839 446841 446847 446853 446857 446859 446863 446869 446871 446877 446881 446883 446887 446889 446893 446895 446897 446898 446899 446901 446902 446903 446905 446907 446911 446913 446917 446919 446923 446929 446931 446937 446941 446943 446947 446953 446959 446961 446967 446971 446973 446979 446983 446989 446997 447348
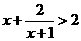 的解集是 ( )
的解集是 ( ) B.
B.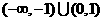
 D.
D.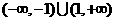
 的圆心到直线
的圆心到直线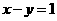 的距离为 ( )
的距离为 ( )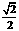 C.1
D.
C.1
D.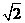
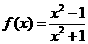 , 则
, 则 ( )
( )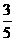 D.
D.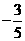
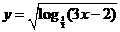 的定义域是 (
)
的定义域是 (
)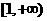 B.
B. C.[
C.[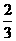 ,1] D.(
,1] D.(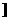
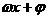 )(A>0,
)(A>0, >0,0<
>0,0<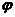 <
<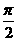 函数,且y=f(x)的最大值为2,其图象相邻两对称轴的距离为2,并过点(1,2).
函数,且y=f(x)的最大值为2,其图象相邻两对称轴的距离为2,并过点(1,2). -1,求f(x)的单调区间。
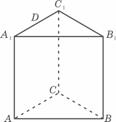
-1,求f(x)的单调区间。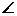 ABC=90°,设AC=2a,BC=a.
ABC=90°,设AC=2a,BC=a.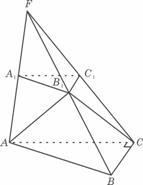
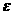 表示取出的3个小球上的最大数字,求:
表示取出的3个小球上的最大数字,求: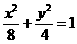 有相同的热点,直线y=
有相同的热点,直线y=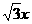 为C的一条渐近线.
为C的一条渐近线.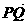 =
=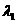
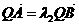 ,且
,且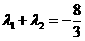 时,求Q点的坐标.
时,求Q点的坐标.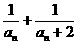 ,求{bn}数列的前项和Sn,并证明Sn+
,求{bn}数列的前项和Sn,并证明Sn+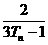 =1.
=1.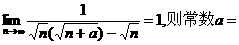 .
.
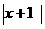 的图象按向量y=(-1,0)平移,得到的图象对应的函数表达式为y=
的图象按向量y=(-1,0)平移,得到的图象对应的函数表达式为y=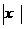
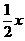 相交,所得弦长为2
相交,所得弦长为2 +
+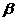 )=
)=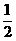 ,则sin(
,则sin(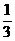 ,则tan
,则tan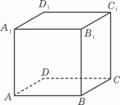

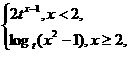
 则不等式f(x)>2的解集为
则不等式f(x)>2的解集为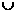 (3,+∞)
(B)(
(3,+∞)
(B)(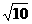 ,+∞)
,+∞)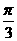 ,a=
,a=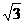 ,b=1,则c=
,b=1,则c=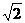 ,焦点到相应准线的距离为1,则该椭圆的离心率为
,焦点到相应准线的距离为1,则该椭圆的离心率为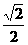 (C)
(C) 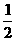 (D)
(D)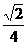
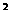 -x-20>0,q:
-x-20>0,q: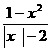 <0,则p是q的
<0,则p是q的 的展开式中第三项与第五项的系数之比为-
的展开式中第三项与第五项的系数之比为-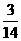 ,其中i
,其中i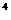 =-1,则展开式中常数项是
=-1,则展开式中常数项是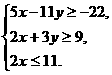 则z=10x+10y的最大值是
则z=10x+10y的最大值是 (B)
(B)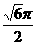 (C)
(C)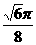 (D)
(D)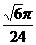
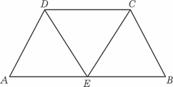
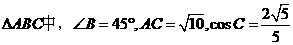 ,求
,求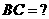
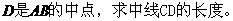
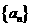 的前n项和为
的前n项和为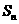 ,
,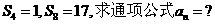
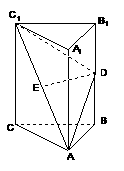 (20)(本小题12分)
(20)(本小题12分)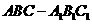 中,
中,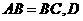 、
、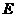 分别为
分别为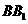 、
、 的中点。
的中点。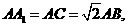 求二面角
求二面角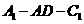 的大小
的大小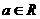 ,函数
,函数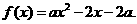 若
若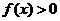 的解集为A,
的解集为A,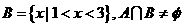 ,求实数
,求实数 的取值范围。
的取值范围。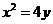 的焦点为F,A、B是抛物线上的两动点,且
的焦点为F,A、B是抛物线上的两动点,且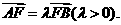 过A、B两点分别作抛物线的切线,设其交点为M。
过A、B两点分别作抛物线的切线,设其交点为M。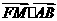 为定值;
为定值;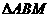 的面积为S,写出
的面积为S,写出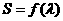 的表达式,并求S的最小值。
的表达式,并求S的最小值。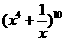 的展开式中常数项是_____。(用数字作答)
的展开式中常数项是_____。(用数字作答)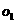 是以
是以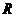 为半径的球
为半径的球 的小圆,若圆
的小圆,若圆 和球
和球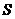 的比为
的比为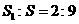 ,则圆心
,则圆心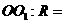 _____。
_____。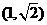 的直线
的直线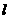 将圆
将圆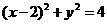 分成两段弧,当劣弧所对的圆心角最小时,直线
分成两段弧,当劣弧所对的圆心角最小时,直线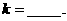
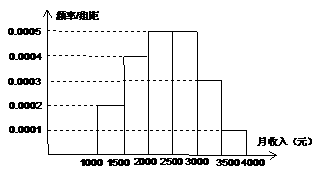 (16)一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如下图)。为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在
(16)一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如下图)。为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在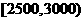 (元)月收入段应抽出_____人。
(元)月收入段应抽出_____人。 =(4,2),向量
=(4,2),向量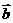 =(
=(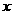 ,3),且
,3),且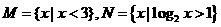 ,则
,则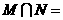 ( )
( )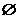 (B)
(B)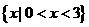 (C)
(C) (D)
(D)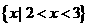
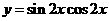 的最小正周期是( )
的最小正周期是( )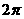 (B)
(B)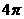 (C)
(C)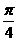 (D)
(D)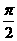
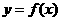 的图像与函数
的图像与函数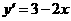 的图像关于坐标原点对称,则
的图像关于坐标原点对称,则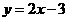 (B)
(B)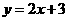 (C)
(C)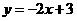 (D)
(D)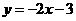
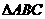 的顶点B、C在椭圆
的顶点B、C在椭圆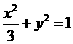 上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则
上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则 (B)6 (C)
(B)6 (C)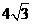 (D)12
(D)12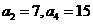 ,则前10项的和
,则前10项的和 =( )
=( )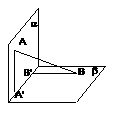 (7)如图,平面
(7)如图,平面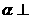 平面
平面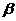 ,
,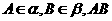 与两平面
与两平面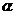 、
、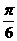 。过A、B分别作两平面交线的垂线,垂足为
。过A、B分别作两平面交线的垂线,垂足为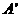 、
、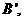 若AB=12,则
若AB=12,则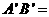 ( )
( )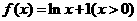 ,则
,则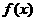 的反函数为( )
的反函数为( )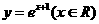 (B)
(B)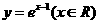
 (D)
(D)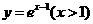
 的一条渐近线方程为
的一条渐近线方程为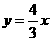 ,则双曲线的离心率为( )
,则双曲线的离心率为( )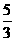 (B)
(B)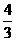 (C)
(C)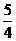 (D)
(D)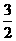
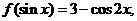 则
则 ( )
( ) (B)
(B)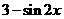 (C)
(C) (D)
(D)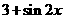
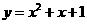 的切线,则其中一条切线为( )
的切线,则其中一条切线为( )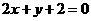 (B)
(B) (C)
(C)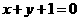 (D)
(D)