0 446767 446775 446781 446785 446791 446793 446797 446803 446805 446811 446817 446821 446823 446827 446833 446835 446841 446845 446847 446851 446853 446857 446859 446861 446862 446863 446865 446866 446867 446869 446871 446875 446877 446881 446883 446887 446893 446895 446901 446905 446907 446911 446917 446923 446925 446931 446935 446937 446943 446947 446953 446961 447348
 设函数
设函数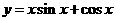 的图象上的点
的图象上的点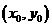 的切线的斜率为
的切线的斜率为 ,若
,若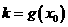 ,则函数
,则函数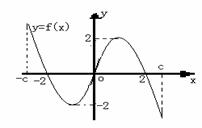
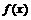 是定义在区间[-c,c]上的奇函数,其图象如图所示:令
是定义在区间[-c,c]上的奇函数,其图象如图所示:令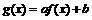 ,则下列关于函数
,则下列关于函数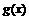 的叙述正确的是[ B
]
的叙述正确的是[ B
]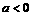 ,则函数
,则函数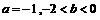 ,则方程
,则方程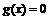 有大于2的实根
有大于2的实根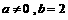 ,则方程
,则方程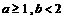 ,则方程
,则方程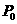 沿与AB夹角为θ的方向射到BC上的点
沿与AB夹角为θ的方向射到BC上的点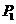 后,依次反射到CD、DA和AB上的点
后,依次反射到CD、DA和AB上的点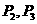 和
和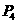 (入射角等于反射角).设
(入射角等于反射角).设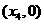 若
若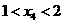 ,则tanθ的取值范围是[
C ]
,则tanθ的取值范围是[
C ]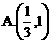
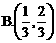
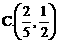
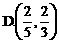
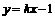 与曲线
与曲线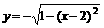 有公共点,则
有公共点,则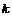 的取值范围是[ D ]
的取值范围是[ D ]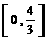 (B)
(B)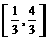 (C)
(C)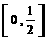 (D)
(D)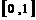
 距离相等,则m值为[ D ]
距离相等,则m值为[ D ]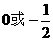 (B)
(B)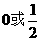 (C)
(C)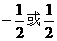 (D)
(D)
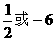
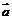 的模等于4,
的模等于4, 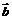 的夹角为,则
的夹角为,则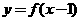 的反函数是
的反函数是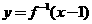 ,则下列等式中正确的是[ B ]
,则下列等式中正确的是[ B ]
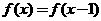 (B)
(B)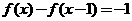
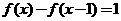 (D)
(D)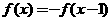
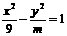 渐近线l方程为
渐近线l方程为 ,则双曲线焦点F到渐近线l的距离为[ C ]
,则双曲线焦点F到渐近线l的距离为[ C ] 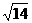 (C)
(C)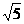 (D)2
(D)2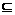 Q
(B)P=Q
(C)P
Q
(B)P=Q
(C)P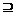 Q
(D)P∩Q=Q
Q
(D)P∩Q=Q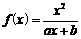 (其中
(其中 、
、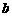 为常数).
为常数).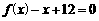 有两个实根
有两个实根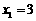 ,
,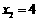 .设
.设 ,
,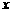 的不等式
的不等式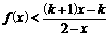 .
.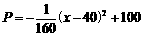 万元.当地政府拟在新的十年发展规划中加快发展此特产的销售,其规划方案为:在规划前后对该项目每年都投入
万元.当地政府拟在新的十年发展规划中加快发展此特产的销售,其规划方案为:在规划前后对该项目每年都投入 万元的销售投资,在未来
万元的销售投资,在未来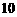 年的前
年的前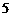 年中,每年都从
年中,每年都从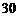 万元用于修建一条公路,
万元用于修建一条公路,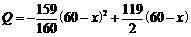 万元.问从
万元.问从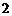 的等边三角形,侧面
的等边三角形,侧面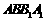 是
是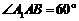 的菱形,且平面
的菱形,且平面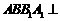 平面
平面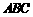 ,
,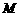 是棱
是棱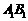 上的动点.
上的动点.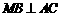 ;
;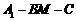 的平面角最小时三棱锥
的平面角最小时三棱锥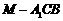 的体积.
的体积.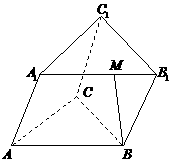
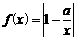 (
(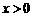 ,
,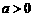 ).
).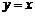 能否为函数
能否为函数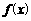 的图象的切线?若能,求出
的图象的切线?若能,求出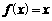 有两个不等的实根
有两个不等的实根 、
、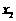 (重根只算一个根),不等式
(重根只算一个根),不等式 对于
对于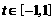 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.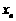 表示某鱼群在第
表示某鱼群在第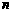 年年初的总量,
年年初的总量,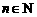 ,且
,且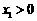 .不考虑其他因素,设在第
.不考虑其他因素,设在第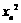 成正比,这些比例系数依次为正常数
成正比,这些比例系数依次为正常数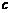 .
.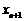 与
与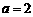 ,
,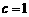 ,为保证对任意
,为保证对任意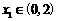 ,都有
,都有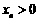 (
(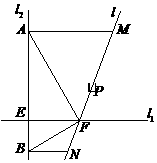 如图所示,
如图所示,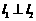 且
且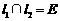 ,
,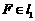 且
且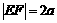 (
(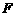 点的任意直线
点的任意直线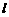 (不与
(不与 重合)交曲线
重合)交曲线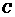 于
于 两点,
两点,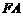 为
为 的角平分线,
的角平分线, (
(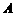 、
、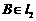 ),
),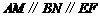 ,
,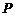 为线段
为线段 的中点.
的中点.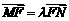 ,证明:
,证明: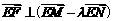 ;
;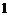 和它自身整除的正整数),且点
和它自身整除的正整数),且点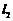 的距离均为非零整数,证明:
的距离均为非零整数,证明: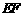 中点的距离不是整数.
中点的距离不是整数.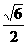 ,且双曲线过点
,且双曲线过点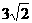 )求双曲线E的方程
)求双曲线E的方程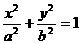 ( a>b>0 )的两焦点为F1( 0
,-c ) ,F2 (
0, c ) ( c> 0 ) ,离心率e=
( a>b>0 )的两焦点为F1( 0
,-c ) ,F2 (
0, c ) ( c> 0 ) ,离心率e=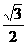 ,焦点到椭圆上的点最短距离为2 -
,焦点到椭圆上的点最短距离为2 -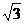 。
。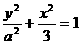 的焦点为F!、F2,离心率为2。
的焦点为F!、F2,离心率为2。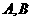 分别是椭圆
分别是椭圆 长轴的左、右端点,点
长轴的左、右端点,点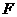 是椭圆的右焦点.点
是椭圆的右焦点.点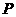 在椭圆上,且位于
在椭圆上,且位于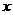 轴的上方,
轴的上方,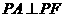 .
.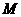 椭圆长轴
椭圆长轴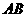 上的一点,
上的一点, 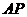 的距离等于
的距离等于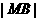 ,求椭圆上的点到点
,求椭圆上的点到点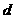 的最小值.
的最小值.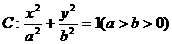 的离心率为
的离心率为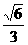 ,F为椭圆在x轴正半轴上的焦点,M、N两点在椭圆C上,且
,F为椭圆在x轴正半轴上的焦点,M、N两点在椭圆C上,且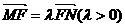 ,定点A(-4,0).
,定点A(-4,0).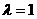 时
时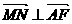 ;
;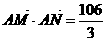 ,求椭圆C的方程;
,求椭圆C的方程;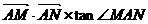 是否有最大值,若存在求出最大值,并求出这时M、N两点所在直线方程,若不存在,给出理由.
是否有最大值,若存在求出最大值,并求出这时M、N两点所在直线方程,若不存在,给出理由.