摘要:22.已知函数=+有如下性质:如果常数>0.那么该函数在0.上是减函数.在.+∞上是增函数. (1)如果函数=+(>0)的值域为6.+∞.求的值, (2)研究函数=+(常数>0)在定义域内的单调性.并说明理由, (3)对函数=+和=+(常数>0)作出推广.使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论.不必证明).并求函数=+(是正整数)在区间[.2]上的最大值和最小值. 解:(1)易知.时.. (2)=+是偶函数.易知.该函数在上是减函数.在上是增函数,则该函数在上是减函数.在上是增函数. (3)推广:函数.当为奇数时..是减函数,.是增函数..是增函数,.是减函数. 当为偶数时..是减函数,.是增函数. .是减函数,.是增函数. =+ 当时.. ∴.是减函数,.是增函数. ∵ ∴函数=+在区间[.2]上的最大值为.最小值为.
网址:http://m.1010jiajiao.com/timu3_id_4469540[举报]
已知函数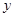 =
=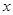 +
+ 有如下性质:如果常数
有如下性质:如果常数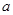 >0,那么该函数在
>0,那么该函数在 0,
0,
 上是减函数,在
上是减函数,在
 ,+∞
,+∞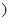 上是增函数.
上是增函数.
(Ⅰ)如果函数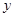 =
=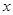 +
+ (
(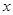 >0)的值域为
>0)的值域为 6,+∞
6,+∞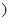 ,求
,求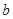 的值;
的值;
(Ⅱ)研究函数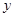 =
=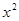 +
+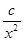 (常数
(常数 >0)在定义域内的单调性,并说明理由;
>0)在定义域内的单调性,并说明理由;
(Ⅲ)对函数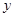 =
=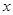 +
+ 和
和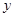 =
=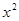 +
+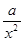 (常数
(常数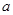 >0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数
>0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数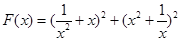 (
(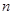 是正整数)在区间[
是正整数)在区间[ ,2]上的最大值和最小值(可利用你的研究结论).
,2]上的最大值和最小值(可利用你的研究结论).
查看习题详情和答案>>
已知函数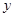 =
=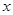 +
+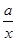 有如下性质:如果常数
有如下性质:如果常数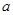 >0,那么该函数在
>0,那么该函数在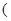 0,
0,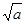
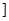 上是减函数,在
上是减函数,在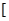
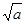 ,+∞
,+∞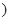 上是增函数.
上是增函数.
(Ⅰ)如果函数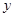 =
=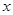 +
+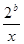 (
(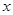 >0)的值域为
>0)的值域为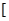 6,+∞
6,+∞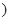 ,求
,求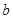 的值;
的值;
(Ⅱ)研究函数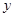 =
=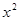 +
+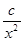 (常数
(常数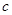 >0)在定义域内的单调性,并说明理由;
>0)在定义域内的单调性,并说明理由;
(Ⅲ)对函数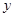 =
=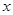 +
+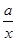 和
和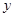 =
=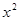 +
+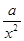 (常数
(常数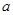 >0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数
>0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数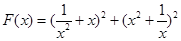 (
(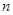 是正整数)在区间[
是正整数)在区间[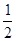 ,2]上的最大值和最小值(可利用你的研究结论).
,2]上的最大值和最小值(可利用你的研究结论).
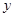 =
=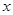 +
+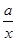 有如下性质:如果常数
有如下性质:如果常数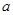 >0,那么该函数在
>0,那么该函数在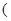 0,
0,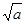
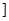 上是减函数,在
上是减函数,在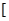
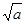 ,+∞
,+∞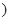 上是增函数.
上是增函数.(Ⅰ)如果函数
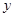 =
=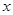 +
+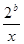 (
(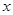 >0)的值域为
>0)的值域为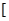 6,+∞
6,+∞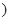 ,求
,求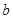 的值;
的值;(Ⅱ)研究函数
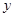 =
=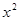 +
+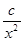 (常数
(常数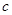 >0)在定义域内的单调性,并说明理由;
>0)在定义域内的单调性,并说明理由;(Ⅲ)对函数
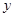 =
=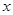 +
+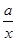 和
和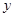 =
=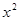 +
+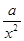 (常数
(常数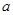 >0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数
>0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数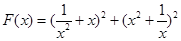 (
(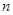 是正整数)在区间[
是正整数)在区间[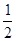 ,2]上的最大值和最小值(可利用你的研究结论).
,2]上的最大值和最小值(可利用你的研究结论).已知函数y=x+![]() 有如下性质:如果常数a>0,那么该函数在(0,
有如下性质:如果常数a>0,那么该函数在(0,![]() ]上是减函数,在[
]上是减函数,在[![]() ,+∞)上是增函数.
,+∞)上是增函数.
(1)如果函数y=x+![]() (x>0)的值域为[6,+∞),求b的值;
(x>0)的值域为[6,+∞),求b的值;
(2)研究函数y=x2+![]() (常数c>0)在定义域内的单调性,并说明理由;
(常数c>0)在定义域内的单调性,并说明理由;
(3)对函数y=x+![]() 和y=x2+
和y=x2+![]() (常数a>0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),
(常数a>0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),