18.(本小题满分12分)
甲、乙两人在罚球线投球命中的概率分别为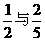 ,投中得1分,投不中得0分.
,投中得1分,投不中得0分.
(Ⅰ)甲、乙两人在罚球线各投球一次,求两人得分之和ξ的数学期望;
(Ⅱ)甲、乙两人在罚球线各投球二次,求这四次投球中至少一次命中的概率;
解:(Ⅰ)依题意,记“甲投一次命中”为事件A,“乙投一次命中”为事件B,则
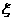 |
0 |
1 |
2 |
|
P |
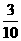 |
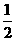 |
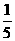 |
P(A)=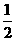 ,P(B)=
,P(B)=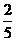 ,P(
,P( )=
)=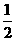 ,P(
,P(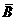 )=
)=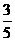 ,甲、乙两人得分之和
,甲、乙两人得分之和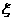 的可取值为0、1、2,则
的可取值为0、1、2,则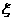 概率分布为
概率分布为
E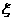 =0×
=0×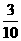 +1×
+1×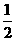 +2×
+2×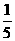 =
=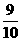
答:甲、乙两人在罚球线各投球一次,两人得分之和ξ的数学期望为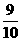
(Ⅱ)∵事件“甲、乙两人在罚球线各投球二次不命中” 的概率是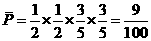
∴甲、乙两人在罚球线各投球二次,至少有一次命中的概率为P=1-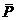 =1-
=1-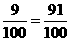
答:甲、乙两人在罚球线各投球二次,至少有一次命中的概率为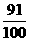 .
.
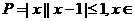 R|,
R|,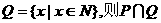 等于 ( )
等于 ( ) ={0,1,2},选(D)
={0,1,2},选(D)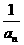 我们知道当a取不同的值时,得到不同的数列,如当a=1时,得到无穷数列:
我们知道当a取不同的值时,得到不同的数列,如当a=1时,得到无穷数列:
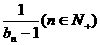 ,求证a取数列{bn}中的任一个数,都可以得到一个有穷数列{an};
,求证a取数列{bn}中的任一个数,都可以得到一个有穷数列{an};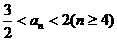 ,求a的取值范围.
,求a的取值范围.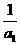 =a2,∴a2=
=a2,∴a2=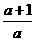 ,
, ,
,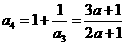 ,
,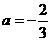 时,
时,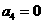
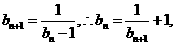
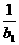 =0
=0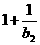 =b1,∴a2=0,
=b1,∴a2=0,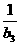 =b2,∴a3=1+
=b2,∴a3=1+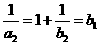 ,∴a4=0,
,∴a4=0,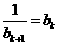 .
.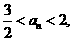 即
即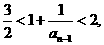 ,∴1<an-1<2.
,∴1<an-1<2.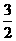 ,2)
,2)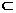 (1,2),
(1,2),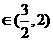 ,都有
,都有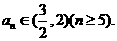
 得
得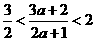 ,
, 得
得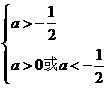 ,故a>0.
,故a>0.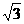 )的直线l过点(0,-2
)的直线l过点(0,-2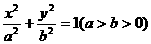 的焦点,且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.
的焦点,且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.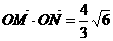 ,
,
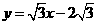 ,
①
,
①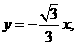 ②
②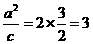 .∵直线ι过椭圆焦点,∴该焦点坐标为(2,0).
.∵直线ι过椭圆焦点,∴该焦点坐标为(2,0).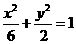 . ③
. ③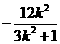 ,x1x2=
,x1x2=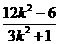 ,
,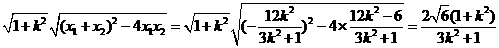
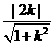 .∵
.∵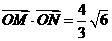 cot∠MON,即
cot∠MON,即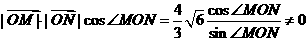 ,
,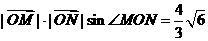 ,∴
,∴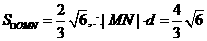 ,
,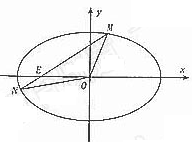
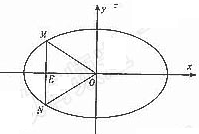 即
即 .整理得
.整理得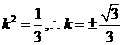 .
.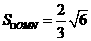
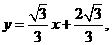 或y=
或y=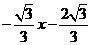 或x=-2.
或x=-2.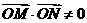 .
.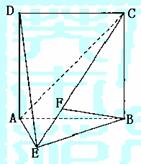 (Ⅰ)求证AE⊥平面BCE;
(Ⅰ)求证AE⊥平面BCE;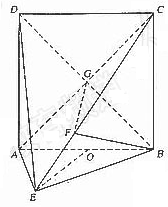
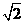 ,
,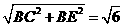 ,BF=
,BF=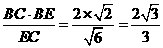
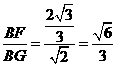 ,∴二面角B-AC-E等于arcsin
,∴二面角B-AC-E等于arcsin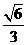 .
. ,∴
,∴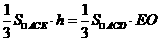 .
.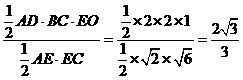 .
.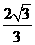 .
.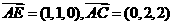
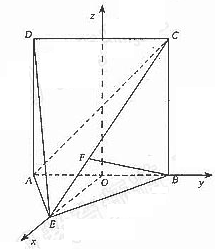 设平面AEC的一个法向量
设平面AEC的一个法向量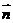 =(x,y,z),则
=(x,y,z),则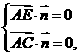 即
即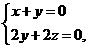 解得
解得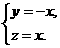
 =(1,0,0),
=(1,0,0),
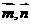 )=
)=
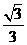 .
. ,∴点D到平面ACE的距离
,∴点D到平面ACE的距离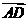 |
|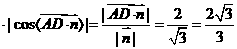 .
.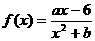 的图象在点M(-1,f(x))处的切线方程为x+2y+5=0.
的图象在点M(-1,f(x))处的切线方程为x+2y+5=0.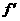 (-1)=
(-1)=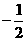 .∵
.∵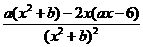 ,∴
,∴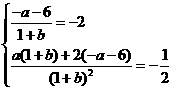
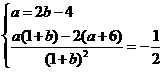 解得a=2,b=3(∵b+1≠0,∴b=-1舍去)
解得a=2,b=3(∵b+1≠0,∴b=-1舍去)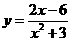
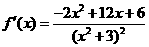 ,令-2x2+12x+6=0,解得x1=
,令-2x2+12x+6=0,解得x1=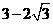 ,x2=
,x2=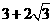
 ;当
;当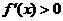 ,
,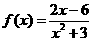 在(-∞,
在(-∞, 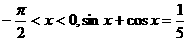 .
.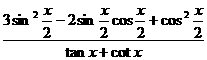 的值.
的值.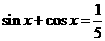 ,得
,得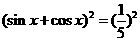 ,得2sinxcosx=
,得2sinxcosx=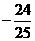 ,∵(sinx-cosxx)2=1-2sinxcosx=
,∵(sinx-cosxx)2=1-2sinxcosx=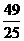 ,又
,又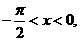 ∴sinx<0cosx>0,∴sinx-cosx=-
∴sinx<0cosx>0,∴sinx-cosx=-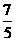
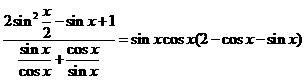
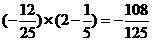
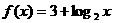 的图象与
的图象与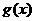 的图象关于
对称,则函数
的图象关于
对称,则函数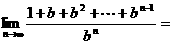 .
. =
=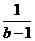
 满足
满足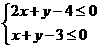 则x+3y的最大值为
。
则x+3y的最大值为
。 如右图,在同一平面直角坐标系中画出下列
如右图,在同一平面直角坐标系中画出下列