17.解:(I)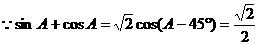
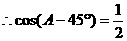 ……………………3分又∵0°<A<180°
……………………3分又∵0°<A<180°
∴A-45°=60°故A=105°………………………………5分
 ……………………7分
……………………7分
(Ⅱ)∵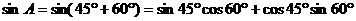
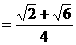 ………9分
………9分
∴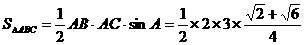
|
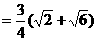 ……12分
……12分
17.解:(I)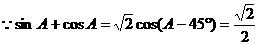
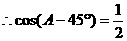 ……………………3分又∵0°<A<180°
……………………3分又∵0°<A<180°
∴A-45°=60°故A=105°………………………………5分
 ……………………7分
……………………7分
(Ⅱ)∵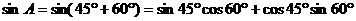
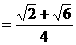 ………9分
………9分
∴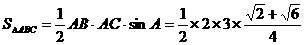
|

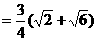 ……12分
……12分