0 445512 445520 445526 445530 445536 445538 445542 445548 445550 445556 445562 445566 445568 445572 445578 445580 445586 445590 445592 445596 445598 445602 445604 445606 445607 445608 445610 445611 445612 445614 445616 445620 445622 445626 445628 445632 445638 445640 445646 445650 445652 445656 445662 445668 445670 445676 445680 445682 445688 445692 445698 445706 447348
 已知
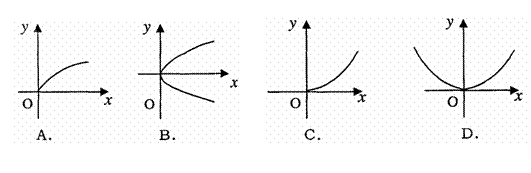
已知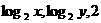 成等差数列,则M(x,y)的轨迹为 ( )
成等差数列,则M(x,y)的轨迹为 ( )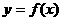 为可导的奇函数,且
为可导的奇函数,且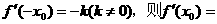 ( )
( )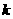 B.
B.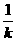 C.-
C.-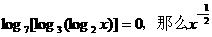 等于 ( )
等于 ( )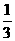 B.
B.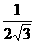 C.
C.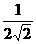 D.
D.
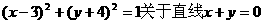 对称的圆的方程是 ( )
对称的圆的方程是 ( )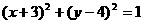 B.
B.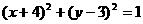
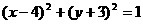 D.
D.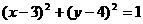
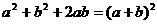 改写成全称命题是 ( )
改写成全称命题是 ( )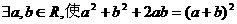
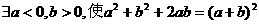
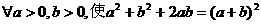
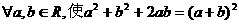
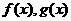 是定义在R上的函数,
是定义在R上的函数,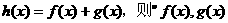 均为偶函数”是“
均为偶函数”是“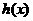 为偶函数”的 ( )
为偶函数”的 ( )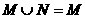 成立的a的值是 ( )
成立的a的值是 ( )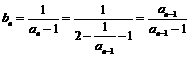 ,而
,而 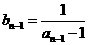 ,
,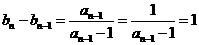 .
.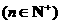
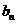 }是首项为
}是首项为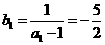 ,公差为1的等差数列.…………… 4分
,公差为1的等差数列.…………… 4分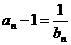 ,而
,而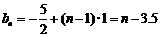 , ∴
, ∴ 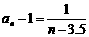 .对于函数
.对于函数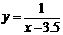 ,在x>3.5时,y>0,
,在x>3.5时,y>0,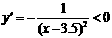 ,在(3.5,
,在(3.5, )上为减函数.
)上为减函数. 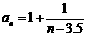 取最大值3. ……………………………… 6分
取最大值3. ……………………………… 6分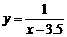 在x<3.5时,y<0,
在x<3.5时,y<0,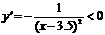 ,在(
,在(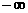 ,3.5)上也为减函数.故当n=3时,取最小值,
,3.5)上也为减函数.故当n=3时,取最小值,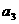 =-1. ……………………………………… 8分
=-1. ……………………………………… 8分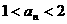 ,再证明
,再证明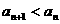
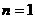 时,
时,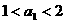 成立; ……………………………………… 9分
成立; ……………………………………… 9分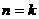 时命题成立,即
时命题成立,即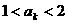 ,
,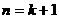 时,
时,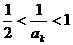
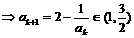
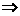
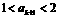
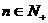 时成立,即
时成立,即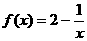 (1≤
(1≤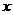 ≤2),则
≤2),则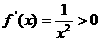 ,
,
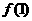
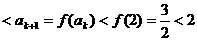 ).
).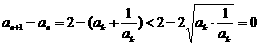
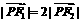 ,
,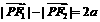 ,∴
,∴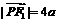 ,
,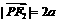 .
. 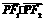 =0,∴(4a)2+(2a)2=(2c)2,∴
=0,∴(4a)2+(2a)2=(2c)2,∴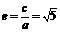 .…………………4分
.…………………4分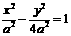 ,渐近线方程为
,渐近线方程为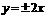 .……5分
.……5分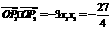 ,∴
,∴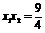 . ∵
. ∵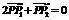 ,∴
,∴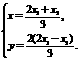 …………10分
…………10分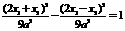 .
.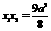 .∴
.∴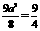 .∴
.∴ 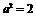 .∴双曲线的方程为
.∴双曲线的方程为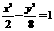 …………12分
…………12分