0 445452 445460 445466 445470 445476 445478 445482 445488 445490 445496 445502 445506 445508 445512 445518 445520 445526 445530 445532 445536 445538 445542 445544 445546 445547 445548 445550 445551 445552 445554 445556 445560 445562 445566 445568 445572 445578 445580 445586 445590 445592 445596 445602 445608 445610 445616 445620 445622 445628 445632 445638 445646 447348
 如图,将网格中的三条线段沿网格线上下或左右平移,组成一个首尾相连的三角形,则三条线段一共至少需要移动D
如图,将网格中的三条线段沿网格线上下或左右平移,组成一个首尾相连的三角形,则三条线段一共至少需要移动D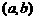 和
和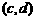 ,定义运算
,定义运算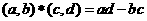 ,若
,若 ,则复数
,则复数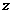 为
为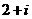 B.
B. 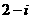 C.
C.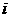 D.
D.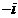
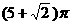
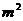 B.
B.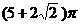
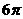
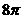
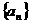 中,如果
中,如果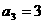 ,
,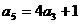 ,那么
,那么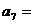
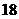 B.
B. C.
C. D.
D.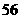

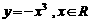 B.
B.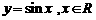
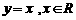 D.
D. 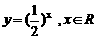
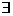 实数x,使
实数x,使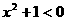 ”的否定可以写成
”的否定可以写成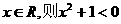 B.
B.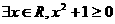
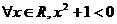 D.
D.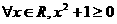
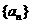 的前
的前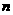 项和
项和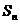 满足:
满足: ,
,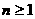 .
.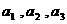 ;
;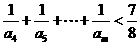 .
.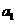 ,第二组为
,第二组为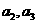 ,第三组为
,第三组为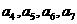 ,第四组
,第四组 ,第
,第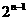 项组成,并把第
项组成,并把第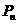
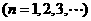 ,已知
,已知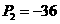 ,
,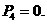
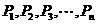 为项构成数列
为项构成数列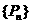 ,试求
,试求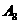 (写出具体数值).
(写出具体数值).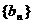 满足:
满足: ,且数列
,且数列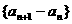
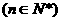 是等差数列,{bn-2}是等比数列.
是等差数列,{bn-2}是等比数列. 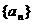 ,
,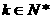 ,使
,使 .若存在,求出k;若不存在,说明理由.
.若存在,求出k;若不存在,说明理由.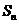 ,设
,设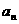 是
是 中,
中,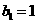 ,点
,点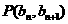 在直线
在直线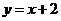 上.
上. 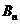 ,比较
,比较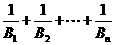 与2的大小;
与2的大小; ,是否存在正整数
,是否存在正整数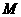 ,使得
,使得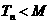 对一切正整数
对一切正整数