0 445590 445598 445604 445608 445614 445616 445620 445626 445628 445634 445640 445644 445646 445650 445656 445658 445664 445668 445670 445674 445676 445680 445682 445684 445685 445686 445688 445689 445690 445692 445694 445698 445700 445704 445706 445710 445716 445718 445724 445728 445730 445734 445740 445746 445748 445754 445758 445760 445766 445770 445776 445784 447348
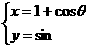 的中心到直线
的中心到直线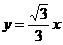 的距离是
的距离是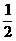 B.
B.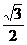 C.1 D.
C.1 D.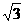
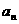 }、{
}、{ 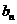 }满足:
}满足: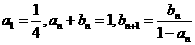 .
.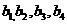 ;
;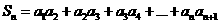 ,求实数a为何值时
,求实数a为何值时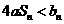 恒成立.
恒成立.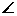 AOB为锐角(O为坐标原点),求实数m的取值范围;
AOB为锐角(O为坐标原点),求实数m的取值范围;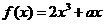 与
与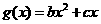 的图象都过点P(2,0),且在点P处有公共切线.
的图象都过点P(2,0),且在点P处有公共切线.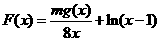 ,其中
,其中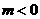 ,求F(x)的单调区间.
,求F(x)的单调区间. 如图,O、H分别为AE、AB的中点.
如图,O、H分别为AE、AB的中点.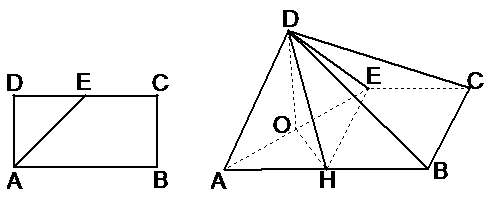 (2)求证:面ADE⊥面ABCE;
(2)求证:面ADE⊥面ABCE;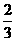 .
. ,求随机变量
,求随机变量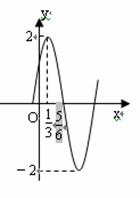 (1)试确定f(x)的解析式;
(1)试确定f(x)的解析式; 和⊙O相交于
和⊙O相交于 和
和 ,
,  切⊙O于
切⊙O于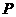 ,
,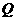 和
和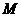 ,交
,交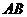 的延长线于
的延长线于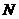 ,
,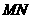 =
=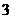 ,
, =15,则
=15,则 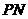 =__________.
=__________.