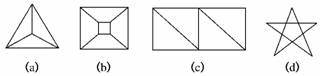
13.下面的(a)、(b)、(c)、(d)为四个平面图.
(1)数一数,每个平面图各有多少个顶点?多少条边?它们分别围成了多少个区域?请将结果填入下表(按填好的例子做).
|
|
顶点数 |
边数 |
区域数 |
|
(a) |
4 |
6 |
3 |
|
(b) |
|
|
|
|
(c) |
|
|
|
|
(d) |
|
|
|
(2)观察上表,推断一个平面图的顶点数、边数、区域数之间有什么关系?
(3)现已知某个平面图有2008个顶点,且围成了2008个区域,试根据以上关系确定这个平面图的边数.
解:(1)填表如下:
|
|
顶点数 |
边数 |
区域数 |
|
(a) |
4 |
6 |
3 |
|
(b) |
8 |
12 |
5 |
|
(c) |
6 |
9 |
4 |
|
(d) |
10 |
15 |
6 |
(2)由上表可以看出,所给的四个平面图的顶点数、边数及区域数之间有下述关系:
4+3-6=1
8+5-12=1
6+4-9=1
10+6-15=1
由此,我们可以推断:任何平面图的顶点数、边数及区域数之间,都有下述关系:
顶点数+区域数-边数=1.
(3)由(2)中所得出的关系,可知所求平面图的边数为:
边数=顶点数+区域数-1=2008+2008-1=4015
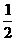 ,
,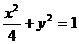 的两个焦点为F1、F2,过F1作垂直于x轴的直线与椭圆相交,一个交点
的两个焦点为F1、F2,过F1作垂直于x轴的直线与椭圆相交,一个交点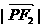 = ( )
= ( )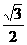 B.
B.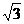 C.
C.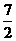 D.4
D.4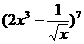 的展开式中常数项是 ( )
的展开式中常数项是 ( )
 6.设A、B、I均为非空集合,且满足A
6.设A、B、I均为非空集合,且满足A B
B 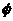 D.( I A)∪( I B)= I B
D.( I A)∪( I B)= I B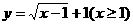 的反函数是 ( )
的反函数是 ( )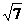 B.
B.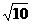 C.
C.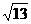 D.4
D.4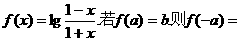 ( )
( )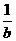 D.-
D.-