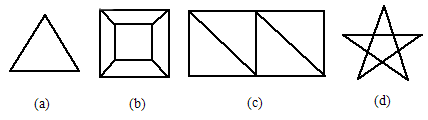
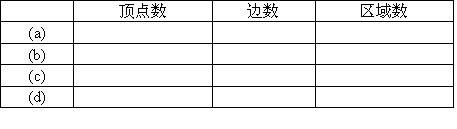
摘要:13.下面的为四个平面图. (1)数一数.每个平面图各有多少个顶点?多少条边?它们分别围成了多少个区域?请将结果填入下表. 顶点数 边数 区域数 (a) 4 6 3 (b) (c) (d) (2)观察上表.推断一个平面图的顶点数.边数.区域数之间有什么关系? (3)现已知某个平面图有2008个顶点.且围成了2008个区域.试根据以上关系确定这个平面图的边数. 解:(1)填表如下: 顶点数 边数 区域数 (a) 4 6 3 (b) 8 12 5 (c) 6 9 4 (d) 10 15 6 (2)由上表可以看出.所给的四个平面图的顶点数.边数及区域数之间有下述关系: 4+3-6=1 8+5-12=1 6+4-9=1 10+6-15=1 由此.我们可以推断:任何平面图的顶点数.边数及区域数之间.都有下述关系: 顶点数+区域数-边数=1. 中所得出的关系.可知所求平面图的边数为: 边数=顶点数+区域数-1=2008+2008-1=4015
网址:http://m.1010jiajiao.com/timu3_id_497753[举报]
已知a、b、c、d是四条互不重合的直线,且c、d分别为a、b在平面α上的射影,给出下面的两组四个论断:
第一组:①a⊥b ②a∥b
第二组:③c⊥d ④c∥d
分别从两组中各选一个论断,使一个作为条件,另一个作为结论,写出一个正确的命题:________.
查看习题详情和答案>>设
、
、
是任意的非零平面向量,且互不平行,则下列四个命题中的真命题是( )
①(
•
)
-(
•
)
=
; ②|
|-|
|<|
-
|;
③(
•
)
-(
•
)
与
垂直; ④λ
+μ
=
?λ=0,μ=0(λ,μ为实数).
查看习题详情和答案>>
| a |
| b |
| c |
①(
| a |
| b |
| c |
| c |
| a |
| b |
| 0 |
| a |
| b |
| a |
| b |
③(
| b |
| c |
| a |
| c |
| a |
| b |
| c |
| a |
| b |
| 0 |
| A.①②③ | B.②③④ | C.①③④ | D.①②③④ |
已知a、b、c表示不同的直线, α、β、γ表示不同的平面, 则下列四个命题中真命题的个数为
[ ]
①若a⊥c, b⊥c, 则a∥b,
②若c⊥α, c⊥β, 则α∥β,
③若a⊥b, b⊥α, 且aα, 则a∥α,
④若α⊥γ, β⊥γ, 则α∥β
A. 1个 B. 2个 C. 3个 D. 4个
查看习题详情和答案>>