3.设m、n是两条不同的直线,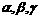 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若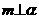 ,
,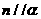 ,则
,则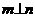 ②若
②若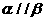 ,
,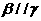 ,
,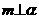 ,则
,则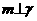
③若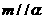 ,
,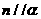 ,则
,则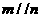 ④若
④若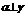 ,
,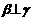 ,则
,则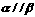
其中正确命题的序号是 ( )
A.①和② B. ②和③ C. ③和④ D. ①和④
19. (本小题满分14分)
(1)
|
长度ξμm |
29 |
30 |
31 |
|
P |
0.3 |
0.5 |
0.2 |
|
宽度ημm |
19 |
20 |
21 |
|
P |
0.3 |
0.4 |
0.3 |
4分
(2)P(ζ = 96) = 0.3´0.3 = 0.09;
P(ζ = 98) = 0.3´0.4 + 0.5´0.3 = 0.27;
P(ζ = 100) = 0.5´0.4 + 0.2´0.3 + 0.3´0.3 = 0.35;
P(ζ = 102) = 0.2´0.4 + 0.5´0.3 = 0.23;
P(ζ = 104) = 0.2´0.3 = 0.06.
得,周长分布律如下表所示
|
周长μ μm |
96 |
98 |
100 |
102 |
104 |
|
P |
0.09 |
0.27 |
0.35 |
0.23 |
0.06 |
6分
(3)方法1(利用周长的分布计算)
Eμ= 96×0.09+98×0.27+100×0.35+102×0.23+104×0.06=99.8 4分
方法2(利用矩形长与宽的期望计算)
由长和宽的分布率可以算得
Eξ=29×P(ξ=29)+30×P(ξ=30)+31×P(ξ=31)
=29×0.3+30×0.5+31×0.2=29.9
Eη=19×P(η=19)+20×P(η=20)+21×P(η=21)
=19×0.3+20×0.4+21×0.3=20
由期望的性质可得
Eμ=2(Eξ+Eη)=2×(29.9+20)=99.8 4分
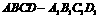 中,P是侧面
中,P是侧面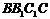 内一动点,若P到直线BC与
内一动点,若P到直线BC与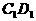 的距离相等,则动点P的轨迹所在的曲线是 ( )
的距离相等,则动点P的轨迹所在的曲线是 ( )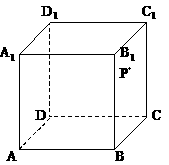
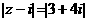 的复数z在复平面上对应点的轨迹是 ( )
的复数z在复平面上对应点的轨迹是 ( )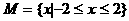 ,
,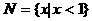 ,则
,则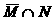 等于( )
等于( )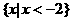 B.
B.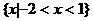 C.
C.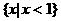 D.
D.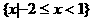
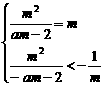 , 得
, 得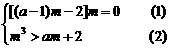 2分
2分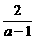 ,
,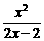 ( x ¹ 1).
3分
( x ¹ 1).
3分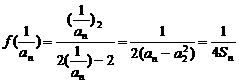
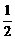 ak(1 – ak) + a k + 1 =
ak(1 – ak) + a k + 1 = 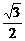 b |2 = |
(
b |2 = |
(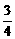 3 分
3 分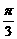 ) +
) +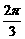 , ∴–
, ∴–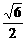 ).
2分
).
2分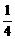 | a |2 –
| a |2 – 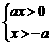 ,得a > 0 , x > 0 . 3
分
,得a > 0 , x > 0 . 3
分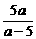 . 2分
. 2分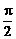 < C – A <
< C – A <