摘要:12.在△ABC中.AB⊥AC.AD⊥BC于D.求证:=+.那么在四面体ABCD中.类比上述结论.你能得到怎样的猜想.并说明理由. 解:如图(1)所示.由射影定理AD2=BD·DC.AB2=BD·BC.AC2=BC·DC. ∴= ==. 又BC2=AB2+AC2. ∴==+. 所以=+. 猜想:类比AB⊥AC.AD⊥BC猜想 四面体ABCD中.AB.AC.AD两两垂直.AE⊥平面BCD.则=++. 如图(2).连接BE交CD于F.连接AF. ∵AB⊥AC.AB⊥AD. ∴AB⊥平面ACD. 而AF⊂面ACD. ∴AB⊥AF. 在Rt△ABF中. AE⊥BF. ∴=+. 在Rt△ACD中.AF⊥CD. ∴=+. ∴=++.故猜想正确.
网址:http://m.1010jiajiao.com/timu3_id_497752[举报]
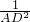 =
=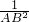 +
+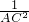 ,那么在四面体A-BCD中,类比上述结论,你能得到怎样的猜想,并说明理由.
,那么在四面体A-BCD中,类比上述结论,你能得到怎样的猜想,并说明理由.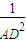 =
=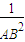 +
+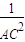 ,那么在四面体A-BCD中,类比上述结论,你能得到怎样的猜想,并说明理由.
,那么在四面体A-BCD中,类比上述结论,你能得到怎样的猜想,并说明理由. =
=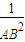 +
+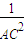 ,那么在四面体A-BCD中,类比上述结论,你能得到怎样的猜想,并说明理由.
,那么在四面体A-BCD中,类比上述结论,你能得到怎样的猜想,并说明理由.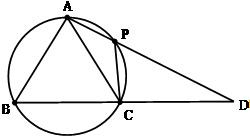 在△ABC中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D.
在△ABC中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D.