4.把等腰直角△ABC沿斜边上的高AD折成直二面角B-AD-C，则BD与平面ABC所成角的正切值为 (　)

A.　　B.　　　 C.1　　D.

解析：如图，在面ADC中，过D作DE⊥AC，交AC于点E.

连接BE，因为二面角B-AD-C为直二面角，所以BD⊥平面ADC，故BD⊥AC.

由以上可知，AC⊥平面BDE，所以平面BDE⊥平面ABC，故∠DBE就是BD与平面ABC所成角，在Rt△DBE中，易求tan∠DBE＝，故选B.

答案：B

3.(改编题)设P是△ABC所在平面外一点，P到△ABC各顶点的距离相等，而且P到△ABC各边的距离也相等，那么△ABC(　)

A.是非等腰的直角三角形

B.是等腰直角三角形

C.是等边三角形

D.不是A、B、C所述的三角形

解析：设O是点P在平面ABC内的射影，因为P到△ABC各顶点的距离相等，所以O是三角形的外心，又P到△ABC各边的距离也相等，所以O是三角形的内心，故△ABC是等边三角形，选C.

答案：C

2.若m、n是两条不同的直线，α、β、γ是三个不同的平面，则下列命题中的真命题是(　)

A.若m⊂β，α⊥β，则m⊥α

B.若α∩γ＝m，β∩γ＝n，m∥n，则α∥β

C.若m⊥β，m∥α，则α⊥β

D.若α⊥γ，α⊥β，则β⊥γ

解析：两平面垂直并不能得到一个平面内的任一直线都与另一平面垂直，故A为假命题；以三棱柱的侧面和侧棱为例知B为假命题；若α⊥γ，α⊥β，则β⊥γ或β∥γ，故D为假命题；若m∥α，则α中必存在直线l与m平行，又m⊥β，∴l⊥β，故α⊥β，故选C.

答案：C

1.教室内任意放一支笔直的铅笔，则在教室的地面上必存在直线与铅笔所在的直线(　)

A.平行　　　　　　 B.相交

C.异面　　　 　　　　　　　　　　 D.垂直

解析：这支铅笔与地面存在三种位置关系，若在地面内，则C排除；若与地面平行则B排除；若与地面相交，则A排除，选D.

答案：D

13．要分析学生初中升学的数学成绩对高一年级数学学习有什么影响，在高一年级学生中随机抽选10名学生，分析他们入学的数学成绩和高一年级期末数学考试成绩，如下表所示：

表中x是学生入学数学成绩，y是指高一年级期末考试数学成绩．

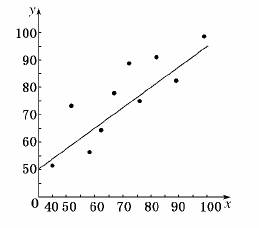
(1)画出散点图；

(2)求回归直线方程；

(3)若某学生王明亮的入学数学成绩为80分，试预测他在高一年级期末考试中的数学成绩为多少？

解：(1)作出散点图如图所示，从散点图可以看出，这两个变量具有线性相关关系．

(2)

可求得＝(63+67+…+76)＝70，

＝(65+78+…+75)＝75.

b＝≈0.721，

∴a＝75－0.721×70≈24.53.

所求的线性回归方程为

＝0.721x+24.53.

(3)若王明亮入学数学成绩为80分，代入上面的线性回归方程

＝0.721x+24.53可得≈82分．

12．据报道，某公司的33名职工的月工资(以元为单位)如下：

(1)求该公司职工月工资的平均数、中位数、众数；

(2)假设副董事长的工资从5000元提升到20000元，董事长的工资从5500元提升到30000元，那么新的平均数、中位数、众数又是什么？(精确到元)

(3)你认为哪个统计量更能反映这个公司员工的工资水平？结合此问题谈一谈你的看法．

解：(1)平均数是＝1500+

≈1500+591＝2091(元)．

中位数是1500元，众数是1500元．

(2)平均数是′＝1500+

≈1500+1788＝3288(元)．

中位数是1500元，众数是1500元．

(3)在这个问题中，中位数或众数均能反映该公司员工的工资水平．因为公司中少数人的工资额与大多数人的工资额差别较大，这样导致平均数与中位数偏差数大，所以平均数不能反映这个公司员工的工资水平．

11．一个地区共有5个乡镇30000人，其中人口比例为3?2?5?1?4，要从这30000人中抽取300个人进行某种传染病分析，因考虑该传染病与不同地理位置及水土有关，问应采取什么样的抽样方法？写出抽样过程．

解：应采用分层抽样的方法．

具体抽样过程如下：

(1)计算抽样比：＝；

(2)计算各乡镇人口数分别为：×30000＝6000，×30000＝4000，×30000＝10000，×30000＝2000，×30000＝8000；

(3)计算各乡镇抽取的人口数分别为：6000×＝60,4000×＝40,10000×＝100,2000×＝20,8000×＝80；

(4)用系统抽样的方法依次从五个乡镇中抽出60人，40人，100人，20人，80人；

(5)将抽取的个体合在一起，就构成所要抽取的一个样本．

10．某肉食鸡养殖小区某种病的发病鸡只数呈上升趋势，统计近4个月这种病的新发病鸡只数的线性回归分析如下表所示：

如果不加控制，仍按这个趋势发展下去，请预测从9月初到12月底的4个月时间里，该养殖小区这种病的新发病鸡总只数约为________．

解析：由上表可得：＝94.7x+1924.7，当x分别取9,10,11,12时，得估计值分别为：2777,2871.7,2966.4,3061.1，则总只数约为2777+2871.7+2966.4+3061.1≈11676.

答案：11676

9．某地教育部门为了调查学生在数学答卷中的有关信息，从上次考试的10000名考生的数学试卷中用分层抽样的方法抽取500人，并根据这500人的数学成绩画出样本的频率分布直方图(如图)，则10000人的数学成绩在[140,150]段的约是________人．

解析：设500人的数学成绩在[140,150]段的人数为x,10000人的数学成绩在[140,150]段的人数为n.

由样本频率分布直方图知数学成绩在[140,150]段的频率最小矩形的面积，即为0.008×10＝0.08＝，∴x＝40.又样本的个数占总个数的，即每组的抽样比为，

∴＝，∴n＝800.

∴10000人的数学成绩在[140,150]段的约是800人．

答案：800

8．已知总体的各个体的值由小到大依次为2,3,3,7，a，b,12,13.7,18.3,20，且总体的中位数为10.5，若要使该总体的方差最小，则a，b的取值是________和________．

解析：由题意a+b＝21，故平均数＝10.

欲使方差最小，只需使(a－10)²+(b－10)²最小，

又∵(a－10)²+(b－10)²＝a²+b²－20(a+b)+200＝a²+b²－220＝(a+b)²－2ab－220＝221－2ab≥221－2²，当且仅当a＝10.5，b＝10.5时最小，故a＝10.5，b＝10.5时，s²最小．

答案：10.5　10.5