摘要:2.下列命题正确的是( ) A.a与b共线.b与c共线.则a与c也共线 B.任意两个相等的非零向量的始点与终点是一平行四边形的四顶点 C.向量a与b不共线.则a与b都是非零向量 D.有相同起点的两个非零向量不平行 解:由于零向量与任一向量都共线.所以A不正确,由于数学中研究的向量是自由向量.所以两个相等的非零向量可以在同一直线上.而此时就构不成四边形.根本不可能是一个平行四边形的四个顶点.所以B不正确,向量的平行只要方向相同或相反即可.与起点是否相同无关.所以D不正确,对于C.其条件以否定形式给出.所以可从其逆否命题来入手考虑.假若a与b不都是非零向量.即a与b至少有一个是零向量.而由零向量与任一向量都共线.可有a与b共线.不符合已知条件.所以有a与b都是非零向量.所以应选C. 考点二: 向量的加.减法 题型1: 考查加加.减法运算及相关运算律 [例2] 化简 [解题思路]:考查向量的加.减法.及相关运算律. 解法一 = = 解法二(利用) = = = 解法三(利用) 设O是平面内任意一点.则= = = [名师指引]掌握向量加减的定义及向量加法的交换律.结合律等基础知识.在求解时需将杂乱的向量运算式有序化处理.必要时也可化减为加.减低出错律. 题型2: 结合图型考查向量加.减法 [例3] 在所在的平面上有一点.满足 .则与的面积之比是( ) A. B. C. D. [解题思路]: 本题中的已知向量都集中体现在三角形中.为此.可充分利用向量加减法的三角形法则实施求解. [解析]由,得, 即,所以点是边上的第二个三等分点,如图所示. 故. [名师指引]三角形中两边对应向量已知.可求第三边所对应的向量.值得注意的是.向量的方向不能搞错.当向量运算转化成代数式运算时.其运算过程可仿照多项式的加减运算进行. [新题导练]
网址:http://m.1010jiajiao.com/timu3_id_497535[举报]
下列命题正确的是
- A.a与b共线,b与c共线,则a与c也共线
- B.任意两个相等的非零向量的始点与终点是一平行四边形的四顶点
- C.向量a与b不共线,则a与b都是非零向量
- D.有相同起点的两个非零向量不平行
 与
与 是共线向量,
是共线向量, 是共线向量,则
是共线向量,则 则
则 =0
=0
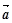 与
与 是单位向量,则
是单位向量,则 的长度与向量
的长度与向量 的长度相等
的长度相等 是共线向量,则A、B、C、D四点共线
是共线向量,则A、B、C、D四点共线 与
与 共线,
共线, 共线,则
共线,则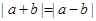 ,则
,则

 与
与 共线,
共线, 共线,则
共线,则 ,则
,则
