摘要: 如图.已知一次函数y = - x +7与正比例函数y = x的图象交于点A.且与x轴交于点B. (1)求点A和点B的坐标, (2)过点A作AC⊥y轴于点C.过点B作直线l∥y轴.动点P从原点O出发.以每秒1个单位长的速度.沿O-C-A的路线向点A运动,同时直线l从点B出发.以相同速度沿x轴向左平移.在平移过程中.直线l交x轴于点R.交线段BA或线段AO于点Q.当点P到达点A时.点P和直线l都停止运动.在运动过程中.设动点P运动的时间为t秒. ①当t为何值时.以A.P.R为顶点的三角形的面积为8? ②是否存在以A.P.Q为顶点的三角形是等腰三角形?若存在.求t的值,若不存在.请说明理由. [答案](1)根据题意.得.解得 .∴A(3.4) . 令y=-x+7=0.得x=7.∴B(7.0). (2)①当P在OC上运动时.0≤t<4. 由S△APR=S梯形COBA-S△ACP-S△POR-S△ARB=8.得 (3+7)×4-×3×(4-t)- t(7-t)- t×4=8 整理,得t2-8t+12=0, 解之得t1=2,t2=6(舍) 当P在CA上运动.4≤t<7. 由S△APR= ×(7-t) ×4=8.得t=3(舍) ∴当t=2时.以A.P.R为顶点的三角形的面积为8. ②当P在OC上运动时.0≤t<4. ∴AP=.AQ=t.PQ=7-t 当AP =AQ时. (4-t)2+32=2(4-t)2, 整理得.t2-8t+7=0. ∴t=1, t=7(舍) 当AP=PQ时.(4-t)2+32=(7-t)2, 整理得.6t=24. ∴t=4 当AQ=PQ时.2(4-t)2=(7-t)2 整理得.t2-2t-17=0 ∴t=1±3 (舍) 当P在CA上运动时.4≤t<7. 过A作AD⊥OB于D,则AD=BD=4. 设直线l交AC于E.则QE⊥AC.AE=RD=t-4.AP=7-t. 由cos∠OAC= = .得AQ = (t-4). 当AP=AQ时.7-t = (t-4).解得t = . 当AQ=PQ时.AE=PE.即AE= AP 得t-4= (7-t).解得t =5. 当AP=PQ时.过P作PF⊥AQ于F AF= AQ = ×(t-4). 在Rt△APF中.由cos∠PAF= = .得AF= AP 即 ×(t-4)= ×(7-t).解得t= . ∴综上所述.t=1或 或5或 时.△APQ是等腰三角形.
网址:http://m.1010jiajiao.com/timu3_id_495586[举报]
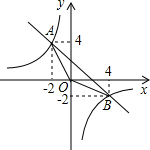 如图,已知一次函数y=kx+b的图象与反比例函数y=
如图,已知一次函数y=kx+b的图象与反比例函数y=| m |
| x |
| A、x<-2或0<x<4 |
| B、-2<x<4 |
| C、x>4或-2<x<0 |
| D、x<-2或x>4 |
 的横坐标和点B的纵坐标都是-2.
的横坐标和点B的纵坐标都是-2. 如图,已知一次函数y=kx+b的图象与反比例函数y=
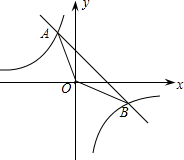
如图,已知一次函数y=kx+b的图象与反比例函数y= 如图,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=
如图,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=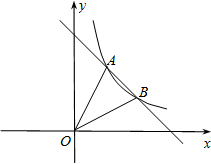 如图,已知一次函数y1=k1x+6与反比例函数
如图,已知一次函数y1=k1x+6与反比例函数