摘要: 如图.直线l经过点A(1.0).且与双曲线y=(x>0)交于点B(2.1).过点P(p.p-1)(p>1)作x轴的平行线分别交曲线y=(x>0)和y=-(x<0)于M.N两点. (1)求m的值及直线l的解析式, (2)若点P在直线y=2上.求证:△PMB∽△PNA, (3)是否存在实数p.使得S△AMN=4S△APM?若存在.请求出所有满足条件的p的值,若不存在.请说明理由. [答案](1)∵点B(2.1)在双曲线y=上. ∴.得m=2. 设直线l的解析式为y=kx+b ∵直线l过A(1.0)和B(2.1) ∴.解得 ∴直线l的解析式为y=x-1. (2) 证明:当x=p时.y=p-1.点P(p.p-1)(p>1) 在直线l上.如图. ∵P(p.p-1)(p>1)在直线y=2上. ∴p-1=2.解得p=3 ∴P(3.2) ∵PN∥x轴.∴P.M.N的纵坐标都等于2 把y=2分别代入双曲线y=和y=.得M(1,2),N ∴.即M是PN的中点. 同理:B是PA的中点. ∴BM∥AN ∴△PMB∽△PNA. (3)由于PN∥x轴.P(p.p-1)(p>1). ∴M.N.P的纵坐标都是p-1(p>1) 把y=p-1分别代入双曲线y=(x>0)和y=-(x<0). 得M的横坐标x=和N的横坐标x=-(其中p>1) ∵S△AMN=4S△APM且P.M.N在同一直线上. ∴,得MN=4PM 即=4(p-).整理得:p2-p-3=0. 解得:p= 由于p>1.∴负值舍去 ∴p= 经检验p=是原题的解. ∴存在实数p.使得S△AMN=4S△APM. p的值为.
网址:http://m.1010jiajiao.com/timu3_id_495482[举报]
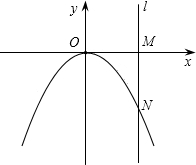 如图,直线l经过点M(3,0),且平行于y轴,与抛物线y=ax2交于点N,若S△OMN=9,则a的值是( )
如图,直线l经过点M(3,0),且平行于y轴,与抛物线y=ax2交于点N,若S△OMN=9,则a的值是( ) 如图,直线l经过点A(-3,1)、B(0,-2),将该直线向右平移2个单位得到直线l′.
如图,直线l经过点A(-3,1)、B(0,-2),将该直线向右平移2个单位得到直线l′. (2012•天河区一模)如图,直线l经过点A(1,0),且与曲线
(2012•天河区一模)如图,直线l经过点A(1,0),且与曲线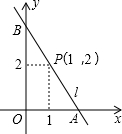 如图,直线l经过点P(1,2),与坐标轴交于A(a,0),B(0,b)两点(其中a<b,如果a+b=6,那么tan∠ABO的值为( )
如图,直线l经过点P(1,2),与坐标轴交于A(a,0),B(0,b)两点(其中a<b,如果a+b=6,那么tan∠ABO的值为( ) (2013•赤峰)如图,直线L经过点A(0,-1),且与双曲线c:y=
(2013•赤峰)如图,直线L经过点A(0,-1),且与双曲线c:y=