摘要: (20011江苏镇江,28,10分)在平面直角坐标系xOy中,直线过点A(1,0)且与y轴平行,直线过点B(0,2)且与x轴平行,直线与相交于P.点E为直线一点,反比例函数的图象过点E且与直线相交于点F. (1)若点E与点P重合,求k的值; (2)连接OE.OF.EF.若k>2,且△OEF的面积为△PEF的面积2倍,求点E的坐标; (3)是否存在点E及y轴上的点M,使得以点M.E.F为顶点的三角形与△PEF全等?若存在,求点E的坐标;若不存在,请说明理由. [答案] (1)k=1×2=2. (2)当k>2时.如图.点E.F分别在P点的右侧和上方过E作x轴的垂线EC.垂足为C.过F作y轴的垂线FD.垂足为D.EC和FD相交于G.则四边形OCGD为矩形. ∵ PF⊥PE. ∴ 四边形OCGD为矩形 ∴ =2 = 解得k=6或2.因为k=2时,E.F重合,所以k=6. 所以E点的坐标为(3,2) (3)存在点E及y轴上的点M,使得△MEF与△PEF全等 ①当k<2时.如图.只可能△MEF≌△PEF. 作FH⊥y轴于H. △FHM∽△MBE得:. ∵FH=1,EM=PE=1-,FM=PF=2-k ∴,BM=, 在Rt△MBE中.由勾股定理得, ∴,解得k=,此时E点的坐标为(.2) ②当k>2时.如图 只可能只可能△MEF≌△PEF.作作FQ⊥y轴于Q. △FQM∽△MBE得: ∵FQ=1,EM=PF=k-2,FM=PE=, ∴,BM=2, 在Rt△MBE中.由勾股定理得, 解得k=或0.但k=0不符合题意.所以k=. 此时E点的坐标为(.2).符合条件的E点坐标为 (.2)和(.2).
网址:http://m.1010jiajiao.com/timu3_id_495488[举报]
如图,在平面直角坐标系xOy中,四边形OABC是长方形,点A,C的坐标分别为(3,0),(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线l:y=-
x+b交折线OAB于点E.
(1)当直线l过点A时,b=
(2)当点E在线段OA上时,判断四边形EABD关于直线DE的对称图形与长方形OABC的重叠部分的图形的形状,并证明你的结论;
(3)若△ODE的面积为s,求s与b的函数关系式,并写出自变量b的取值范围.
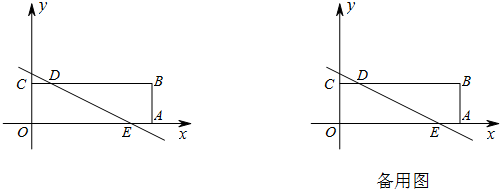
查看习题详情和答案>>
| 1 | 2 |
(1)当直线l过点A时,b=
1.5
1.5
,点D的坐标为(1,1)
(1,1)
;(2)当点E在线段OA上时,判断四边形EABD关于直线DE的对称图形与长方形OABC的重叠部分的图形的形状,并证明你的结论;
(3)若△ODE的面积为s,求s与b的函数关系式,并写出自变量b的取值范围.
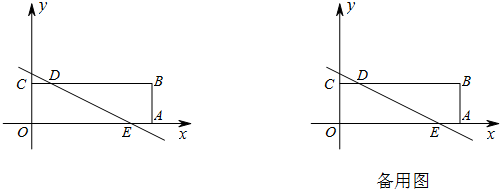
 (2013•西宁)如图,正方形AOCB在平面直角坐标系xoy中,点O为原点,点B在反比例函数y=
(2013•西宁)如图,正方形AOCB在平面直角坐标系xoy中,点O为原点,点B在反比例函数y=| k |
| x |
(1)求反比例函数y=
| k |
| x |
(2)若动点E从A开始沿AB向B以每秒1个单位的速度运动,同时动点F从B开始沿BC向C以每秒2个单位的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动.若运动时间用t表示,△BEF的面积用S表示,求出S关于t的函数关系式,并求出当运动时间t取何值时,△BEF的面积最大?
(3)当运动时间为
| 4 |
| 3 |
在平面直角坐标系xOy中,抛物线y=-
x2+bx+c与x轴交于A、B两点(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,且OA=2,OC=3.
(1)求抛物线的解析式;
(2)若点E在第一象限内的此抛物线上,且OE⊥BC于D,求点E的坐标;
(3)在抛物线的对称轴上是否存在一点P,使线段PA与PE之差的值最大?若存在,请求出这个最大值和点P的坐标;若不存在,请说明理由. 查看习题详情和答案>>
| 1 | 2 |
(1)求抛物线的解析式;
(2)若点E在第一象限内的此抛物线上,且OE⊥BC于D,求点E的坐标;
(3)在抛物线的对称轴上是否存在一点P,使线段PA与PE之差的值最大?若存在,请求出这个最大值和点P的坐标;若不存在,请说明理由. 查看习题详情和答案>>
 已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点A、B,与反比例函数在第一象限内的图象交于点C,CD⊥x轴于点D,OD=3,点A为OD的中点,tan∠OBD=
已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点A、B,与反比例函数在第一象限内的图象交于点C,CD⊥x轴于点D,OD=3,点A为OD的中点,tan∠OBD= (2012•镇江)如图,在平面直角坐标系xOy中,直线AB经过点A(-4,0)、B(0,4),⊙O的半径为1(O为坐标原点),点P在直线AB上,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为
(2012•镇江)如图,在平面直角坐标系xOy中,直线AB经过点A(-4,0)、B(0,4),⊙O的半径为1(O为坐标原点),点P在直线AB上,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为