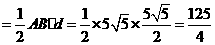0 45365 45373 45379 45383 45389 45391 45395 45401 45403 45409 45415 45419 45421 45425 45431 45433 45439 45443 45445 45449 45451 45455 45457 45459 45460 45461 45463 45464 45465 45467 45469 45473 45475 45479 45481 45485 45491 45493 45499 45503 45505 45509 45515 45521 45523 45529 45533 45535 45541 45545 45551 45559 447348
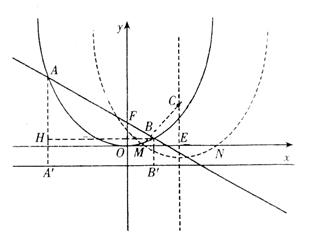
 (3)探索:当点B分别位于l1在x轴上、下两部分的图像上时,平行四边形ABCD的面积是否存在最大值和最小值?若存在,判断它是何种特殊平行四边形,并求出它的面积;若不存在,请说明理由。
(3)探索:当点B分别位于l1在x轴上、下两部分的图像上时,平行四边形ABCD的面积是否存在最大值和最小值?若存在,判断它是何种特殊平行四边形,并求出它的面积;若不存在,请说明理由。 交x轴于A、B两点,
交x轴于A、B两点, ,试探索问题⑵。
,试探索问题⑵。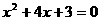 ,解得x1=-3,x2=-1,
,解得x1=-3,x2=-1,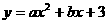
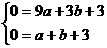
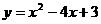
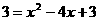 ,则x1=0,x2=4
,则x1=0,x2=4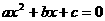
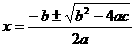 ,
,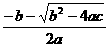 ,0),B点坐标为(
,0),B点坐标为(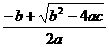 ,0)
,0)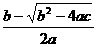 ,0),∴AC=
,0),∴AC=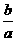
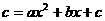 ,x1=0,x2=
,x1=0,x2=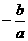
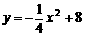 ,BC所在抛物线的解析式为
,BC所在抛物线的解析式为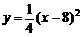 ,且已知
,且已知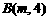 .
.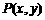 是山坡线AB上任意一点,用y表示x,并求点B的坐标;
是山坡线AB上任意一点,用y表示x,并求点B的坐标; (3)在山坡上的700米高度(点D)处恰好有一小块平地,可以用来建造索道站.索道的起点选择在山脚水平线上的点E处,
(3)在山坡上的700米高度(点D)处恰好有一小块平地,可以用来建造索道站.索道的起点选择在山脚水平线上的点E处,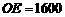 (米).假设索道DE可近似地看成一段以E为顶点、开口向上的抛物线,解析式为
(米).假设索道DE可近似地看成一段以E为顶点、开口向上的抛物线,解析式为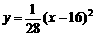 .试求索道的最大悬空高度.
.试求索道的最大悬空高度. ,
, 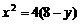 ,
,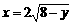
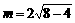 =4,∴
=4,∴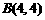
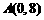
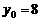 ,得
,得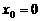 ;令
;令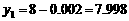 ,得
,得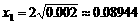
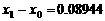 (百米)
(百米)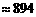 (厘米)
(厘米) 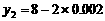 、
、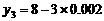 ,可得
,可得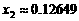 、
、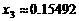
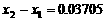 (百米)
(百米)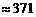 (厘米)
(厘米) 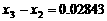 (百米)
(百米)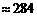 (厘米)
(厘米) 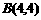 ,又取
,又取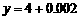 ,则
,则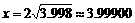
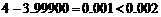
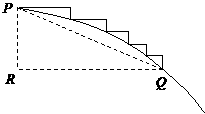 ②另解:连接任意一段台阶的两端点P、Q,如图
②另解:连接任意一段台阶的两端点P、Q,如图
 于H
于H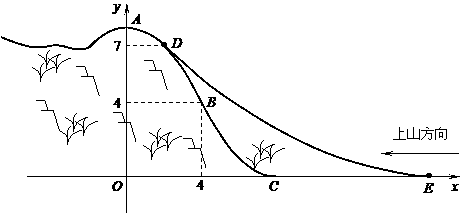 则
则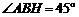 ,又第一级台阶的长大于它的高
,又第一级台阶的长大于它的高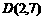 、
、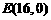 、
、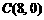
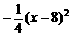
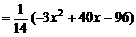
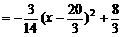
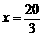 时,
时,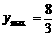
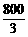 米.
米. 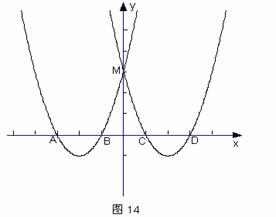
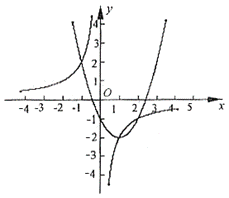
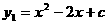 的部分图象如图1所示。
的部分图象如图1所示。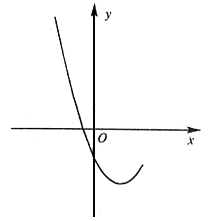
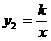 的图象经过(2)中抛物线上点(1,a),试在图2所示直角坐标系中,画出该反比例函数及(2)中抛物线的图象,并利用图象比较
的图象经过(2)中抛物线上点(1,a),试在图2所示直角坐标系中,画出该反比例函数及(2)中抛物线的图象,并利用图象比较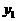 与
与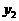 的大小。
的大小。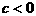
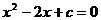 有两个不等的实数根。
有两个不等的实数根。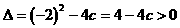 ,且
,且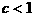
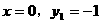 代入
代入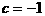
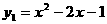
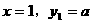 代入
代入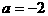
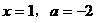 代入
代入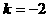
 所以
所以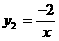
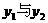 除交点(1,-2)外,还有两个交点大致为
除交点(1,-2)外,还有两个交点大致为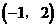 和
和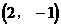
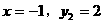 和
和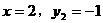 分别代入
分别代入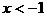 或
或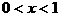 或
或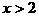 时,
时,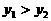
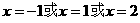 时,
时,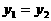
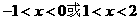 时,
时,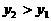
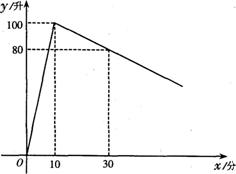 (1)求在第一个加工过程中,油箱中油量y(升)与机器运行时间x(分)之间的函数关系式(不必写出自变量x的取值范围);
(1)求在第一个加工过程中,油箱中油量y(升)与机器运行时间x(分)之间的函数关系式(不必写出自变量x的取值范围);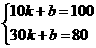
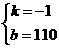
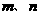 是方程
是方程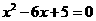 的两个实数根,且
的两个实数根,且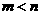 ,抛物线
,抛物线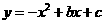 的图像经过点A(
的图像经过点A(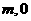 )、B(
)、B(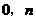 ).
).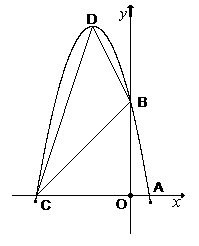 设(1)中抛物线与
设(1)中抛物线与 轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和△BCD的面积;(注:抛物线
轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和△BCD的面积;(注:抛物线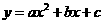
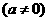 的顶点坐标为
的顶点坐标为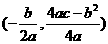 )
)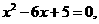 得
得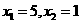
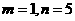
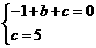 解这个方程组,得
解这个方程组,得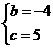
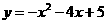
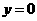 ,得
,得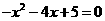
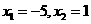
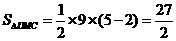
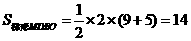 ,
,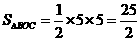
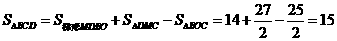 .
.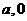 )
)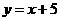 .
.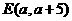 ,
,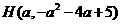 .
.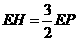 ,即
,即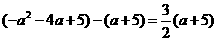
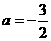 或
或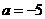 (舍去)
(舍去)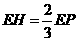 ,即
,即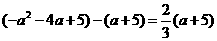
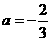 或
或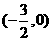 或
或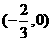 .
. ,对称轴为
,对称轴为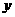 轴.一次函数
轴.一次函数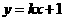 的图象与二次函数的图象交于
的图象与二次函数的图象交于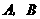 两点(
两点( 在
在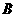 的左侧),且
的左侧),且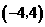 .平行于
.平行于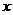 轴的直线
轴的直线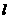 过
过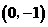 点.
点.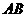 为直径的圆与直线
为直径的圆与直线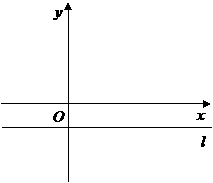 (3)把二次函数的图象向右平移
(3)把二次函数的图象向右平移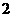 个单位,再向下平移
个单位,再向下平移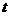 个单位
个单位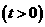 ,二次函数的图象与
,二次函数的图象与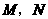 两点,一次函数图象交
两点,一次函数图象交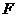 点.当
点.当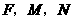 三点的圆的面积最小?最小面积是多少?
三点的圆的面积最小?最小面积是多少?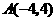 代入
代入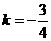 ,
, 一次函数的解析式为
一次函数的解析式为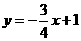 ;
;  二次函数图象的顶点在原点,对称轴为
二次函数图象的顶点在原点,对称轴为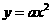 ,
,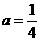 ,
, .
.  (2)由
(2)由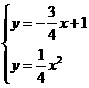
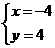 或
或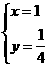 ,
,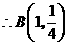 ,
, 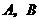 点分别作直线
点分别作直线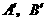 ,
,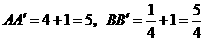 ,
,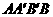 的中位线长为
的中位线长为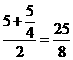 ,
, 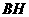 垂直于直线
垂直于直线 于点
于点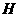 ,则
,则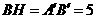 ,
,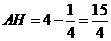 ,
,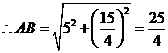 ,
, 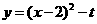 ,
,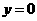 ,得
,得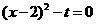 ,
,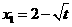 ,
,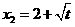 ,
,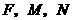 三点的圆的圆心一定在直线
三点的圆的圆心一定在直线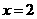 上,点
上,点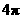 ,
, 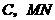 中点为
中点为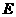 ,连
,连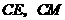 ,则
,则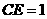 ,
,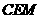 中,
中,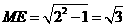 ,
,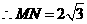 ,而
,而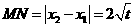 ,
,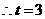 ,
,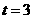 时,过
时,过 是方程
是方程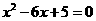 的两个实数根,且
的两个实数根,且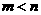 ,抛物线
,抛物线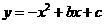 的图像经过点A(
的图像经过点A(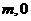 )、B(
)、B(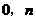 ).
).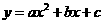
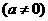 的顶点坐标为(
的顶点坐标为(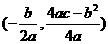 )
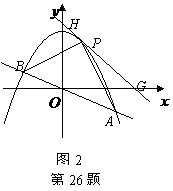
)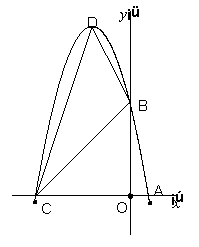 P是线段OC上的一点,过点P作PH⊥
P是线段OC上的一点,过点P作PH⊥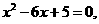 得
得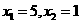
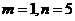
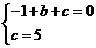 解这个方程组,得
解这个方程组,得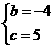
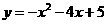
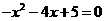
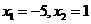
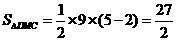
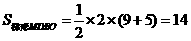 ,
,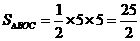
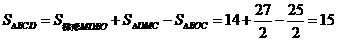 .
.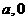 )
)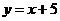 .
.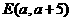 ,
,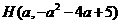 .
.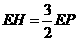 ,即
,即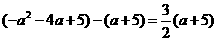
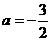 或
或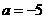 (舍去)
(舍去)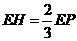 ,即
,即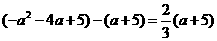
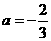 或
或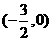 或
或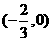 .
.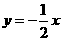 与抛物线
与抛物线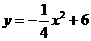 交于
交于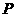 在直线
在直线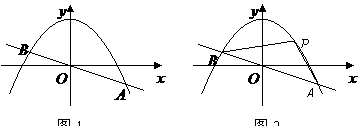
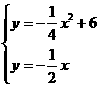 解之得
解之得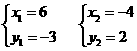
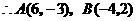
 (2)作
(2)作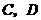 两点,交
两点,交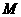 (如图1)
(如图1)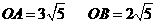
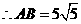
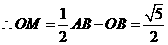
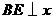 轴,
轴,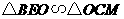 ,得:
,得: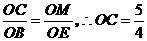 ,
,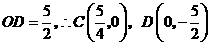
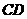 的解析式为
的解析式为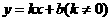
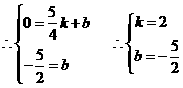
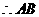 的垂直平分线的解析式为:
的垂直平分线的解析式为: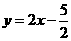 .
.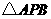 的面积最大,则点
的面积最大,则点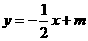 上,并设该直线与
上,并设该直线与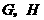 两点(如图2).
两点(如图2).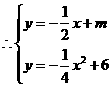
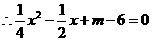
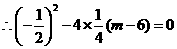 ,
,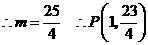
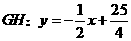 中,
中,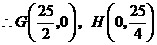
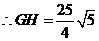
 的距离为
的距离为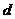 ,
,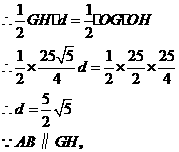
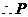 到
到