2. 二次函数中的数形结合[用数形结合思想]
例37(1) 抛物线 y = - 3x2 + 5x - 4开口 ,
y = 4x2 – 6x + 5 开口 .
(2)已知: 二次函数 y = ( m – 3 ) x2 + 2mx + m + 2,其中m 为常数,且满足-2 < m < 3,此抛物线的开口 ,与 x 轴 交点(填有、无),与 y 轴的交点在x 轴 (填上方、下方).
(3) 如果二次函数y = 2x2 + ( 2a – b )x + b,当且仅当
1 < x < 2 时,y < 0,那么 a、b 的值是 .
(4)已知二次函数y=ax2+bx+c,且a<0,a-b+c>0,则一定有 ( )
(A)b2 - 4ac>0 (B)b2 - 4ac=0 (C)b2 - 4ac<0 (D)b2 - 4ac≤0
例38 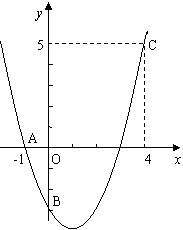 如图,二次函数y=ax2+bx+c的图象经过A、B、C三点.
如图,二次函数y=ax2+bx+c的图象经过A、B、C三点.
1)观察图象写出A、B、C三点的坐标,并求出此二次函数的解析式;
2)求出此抛物线的顶点坐标和对称轴。
|
例39 (1)已知抛物线y=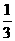 (x - 4)2 - 3的部分图像(如图) 图像再次与x轴相交时的坐标是
( )
(x - 4)2 - 3的部分图像(如图) 图像再次与x轴相交时的坐标是
( )
(A) (5,0) (B) (6,0) (C) (7,0) (D) (8,0)
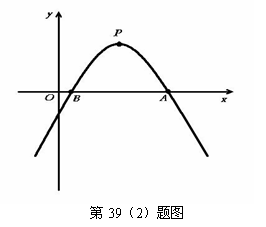
(2)如图,已知二次函数y=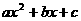 (a≠0)的图象的顶点P的横坐标是4,图象交x轴于点A(m,0)和点B,且m>4,那么AB的长是
( )
(a≠0)的图象的顶点P的横坐标是4,图象交x轴于点A(m,0)和点B,且m>4,那么AB的长是
( )
(A)4+m (B)m (C)2m一8 (D)8-2m
4. 二次函数的应用
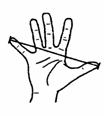 例45 如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距. 某项研究表明,一般情况下人的身高h是指距d的一次函数. 下表是测得的指距与身高的一组数据:
例45 如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距. 某项研究表明,一般情况下人的身高h是指距d的一次函数. 下表是测得的指距与身高的一组数据:
|
指距d(cm) |
20 |
21 |
22 |
23 |
|
身高h(cm) |
160 |
169 |
178 |
187 |
(1) 求出h与d之间的函数关系式(不要求写出自变量d的取值范围):
(2) 某人身高为196cm,一般情况下他的指距应是多少?
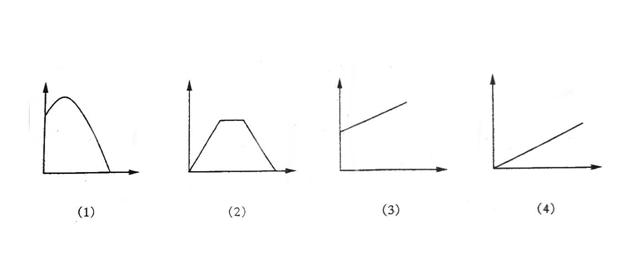 例46若用(1)、(2)、(3)、(4)四幅图像分别表示量之间的关系,请按图像所给顺序,将下面的a、b、c、d对应排序
例46若用(1)、(2)、(3)、(4)四幅图像分别表示量之间的关系,请按图像所给顺序,将下面的a、b、c、d对应排序
(a) 小车从光滑的斜面上滑下(小车速度与时间的关系)
(b) 一个弹簧不挂重物到逐渐挂重物(弹簧长度与所挂重物重量的关系)
(c) 运动员推出去的铅球(铅球高度与时间的关系)
(d) 小杨从A到B后,停留一段时间,然后按原速度返回(路程与时间的关系)
正确的顺序是:( )
(A)(c)(d)(b)(a) (B)(a)(b)(c)(d)
(C)(b)(c)(a)(d) (D)(d)(a)(c)(b)
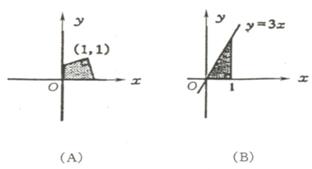
 例32 (1)已知一次函数 y = kx
+ b的图象经过第一、二、四象限,则反比例函数 y =
例32 (1)已知一次函数 y = kx
+ b的图象经过第一、二、四象限,则反比例函数 y = 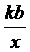 的图象是(
).
的图象是(
). 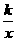 的图象交于M、N两点
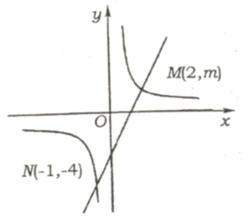
的图象交于M、N两点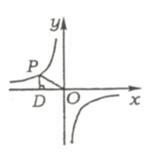 例31如图,点P是反比例函数y =
例31如图,点P是反比例函数y = 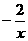 上的一点,PD⊥x轴于点D,则△POD的面积为_______.
上的一点,PD⊥x轴于点D,则△POD的面积为_______.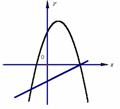
 (A) (B) (C)
(D)
(A) (B) (C)
(D)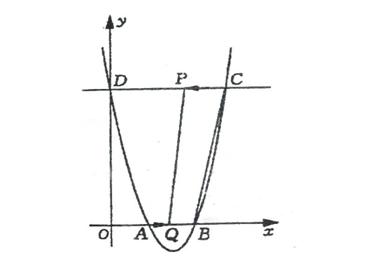 例50如图、已知抛物线y=x2 –ax+a+2与x轴交于A、B两点,与y轴交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C。动点P以每秒2个单位长度的速度从点C出发,沿C→D运动,同时,点Q以每秒1个单位长度的速度从A出发,沿A→B运动。连结PQ、CB.设点P的运动时间为t秒
.
例50如图、已知抛物线y=x2 –ax+a+2与x轴交于A、B两点,与y轴交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C。动点P以每秒2个单位长度的速度从点C出发,沿C→D运动,同时,点Q以每秒1个单位长度的速度从A出发,沿A→B运动。连结PQ、CB.设点P的运动时间为t秒
.
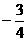 |+(
|+(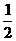 )2
+ 2-1的结果相同的是 ( )
)2
+ 2-1的结果相同的是 ( )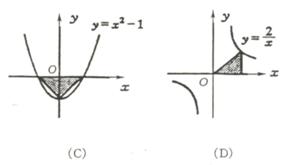
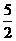 ),(1,6)三点,直线l 的解析式为y=2 x-3.(1)求抛物线G 的函数解析式;(2)求证抛物线G 与直线l 无公共点;(3)若与l 平行的直线y=2 x+m 与抛物线G 只有一个公共点P,求P 点的坐标.
),(1,6)三点,直线l 的解析式为y=2 x-3.(1)求抛物线G 的函数解析式;(2)求证抛物线G 与直线l 无公共点;(3)若与l 平行的直线y=2 x+m 与抛物线G 只有一个公共点P,求P 点的坐标.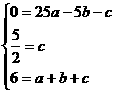 ,
,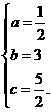
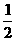 x2+3 x+
x2+3 x+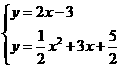 ,
, =0,
=0,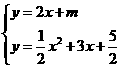 ,消去y,得
,消去y,得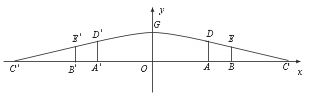
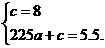
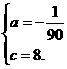
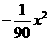 +8.
+8.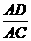 =
=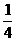 且AD=5.5,
且AD=5.5,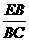 =
=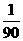 ×16+8=
×16+8=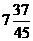 ,而
,而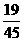 >0,
>0,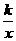 .(1)当k 为何值时,这两个函数的图象有两个交点?k 为何值时,这两个函数的图象没有交点?(2)这两个函数的图象能否只有一个交点?若有,求出这个交点坐标;若没有,请说明理由.
.(1)当k 为何值时,这两个函数的图象有两个交点?k 为何值时,这两个函数的图象没有交点?(2)这两个函数的图象能否只有一个交点?若有,求出这个交点坐标;若没有,请说明理由.