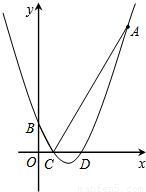
摘要:如图14.抛物线E:交x轴于A.B两点. 交y轴于M点.抛物线E关于y轴对称的抛物线F交x轴于 C.D两点. ⑴求F的解析式, ⑵在x轴上方的抛物线F或E上是否存在一点N.使以A.C N.M为顶点的四边形是平行四边形.若存在.求点N坐标, 若不存在.请说明理由, ⑶若将抛物线E的解析式改为.试探索问题⑵. [解析] 当y=0时..解得x1=-3.x2=-1. ∴A.B点坐标分别为 当x=0时.y=3.∴M点坐标为(0.3).A.B.M三点关于y轴得对称点分别是D.C.M.∴D.C坐标为 设F的解析式为 ∴a=1.b=-4 ∴F的解析式为 (2)存在.假设MN∥AC.∴N点的纵坐标为3. 若在抛物线F上.当y=3时..则x1=0.x2=4 ∴N点坐标为(4.3).∴MN=4. 由(1)可求AC=4.∴MN=AC.∴四边形ACNM为平行四边形. 根据抛物线F和E关于y轴对称.故N点坐标为 (3) 存在.假设MN∥AC.∴N点的纵坐标为c.设y=0.∴ ∴. ∴A点坐标为(.0).B点坐标为(.0) ∴C点坐标为(.0).∴AC= 在抛物线E上.当y=c时..x1=0.x2= ∴N点坐标为(.0) NM=0-()=.∴NM=AC.∴四边形ACMN为平行四边形. 根据抛物线F和E关于y轴对称.故N点坐标为(.c)或(.c).
网址:http://m.1010jiajiao.com/timu3_id_454628[举报]
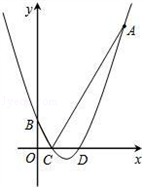
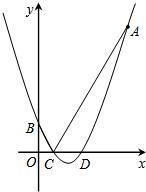 如图,抛物线的顶点坐标是
如图,抛物线的顶点坐标是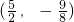 ,且经过点A(8,14).
,且经过点A(8,14).
(1)求该抛物线的解析式;
(2)设该抛物线与y轴相交于点B,与x轴相交于C、D两点(点C在点D的左边),试求点B、C、D的坐标;
(3)设点P是x轴上的任意一点,分别连接AC、BC.试判断:PA+PB与AC+BC的大小关系,并说明理由.
查看习题详情和答案>>
如图,抛物线的顶点坐标是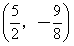 ,且经过点A(8,14)。
,且经过点A(8,14)。
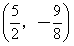 ,且经过点A(8,14)。
,且经过点A(8,14)。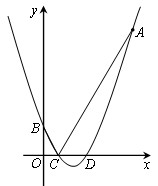
(1)求该抛物线的解析式;
(2)设该抛物线与y轴相交于点B,与x轴相交于C、D两点(点C在点D的左边),试求点B、C、D的坐标;
(3)设点P是x轴上的任意一点,分别连结AC、BC,试判断:PA+PB与AC+BC的大小关系,并说明理由。
查看习题详情和答案>>
(2)设该抛物线与y轴相交于点B,与x轴相交于C、D两点(点C在点D的左边),试求点B、C、D的坐标;
(3)设点P是x轴上的任意一点,分别连结AC、BC,试判断:PA+PB与AC+BC的大小关系,并说明理由。
如图,抛物线的顶点坐标是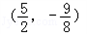 ,且经过点A(8,14).
,且经过点A(8,14).
(1)求该抛物线的解析式;
(2)设该抛物线与y轴相交于点B,与x轴相交于C、D两点(点C在点D的左边),试求点B、C、D的坐标;
(3)设点P是x轴上的任意一点,分别连接AC、BC,试判断:PA+PB与AC+BC的大小关系,并说明理由。
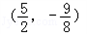 ,且经过点A(8,14).
,且经过点A(8,14).(1)求该抛物线的解析式;
(2)设该抛物线与y轴相交于点B,与x轴相交于C、D两点(点C在点D的左边),试求点B、C、D的坐标;
(3)设点P是x轴上的任意一点,分别连接AC、BC,试判断:PA+PB与AC+BC的大小关系,并说明理由。
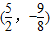 ,且经过点A(8,14).
,且经过点A(8,14).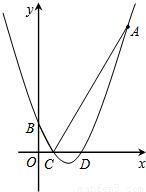
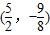 ,且经过点A(8,14).
,且经过点A(8,14).