摘要:已知:是方程的两个实数根.且.抛物线的图像经过点A().B(). (1) 求这个抛物线的解析式, 中抛物线与轴的另一交点为C,抛物线的顶点为D.试求出点C.D的坐标和△BCD的面积,(注:抛物线的顶点坐标为() (3) P是线段OC上的一点.过点P作PH⊥轴.与抛物线交于H点.若直线BC把△PCH分成面积之比为2:3的两部分.请求出P点的坐标. 解:(1)解方程得 由.有 所以点A.B的坐标分别为A. 将A的坐标分别代入. 得解这个方程组.得 所以.抛物线的解析式为 (2)由.令.得 解这个方程.得 所以C点的坐标为.由顶点坐标公式计算.得点D. 过D作轴的垂线交轴于M. 则 . 所以.. (3)设P点的坐标为() 因为线段BC过B.C两点.所以BC所在的值线方程为. 那么.PH与直线BC的交点坐标为. PH与抛物线的交点坐标为. 由题意.得①.即 解这个方程.得或 ②.即 解这个方程.得或 P点的坐标为或.
网址:http://m.1010jiajiao.com/timu3_id_454622[举报]
已知:![]() 是方程
是方程![]() 的两个实数根,且
的两个实数根,且![]() ,抛物线
,抛物线![]() 的图象经过点
的图象经过点![]() .
.
(1)求这个抛物线的解析式;
(2)设点![]() 是抛物线上一动点,且位于第三象限,四边形
是抛物线上一动点,且位于第三象限,四边形![]() 是以
是以![]() 为对角线的平行四边形,求
为对角线的平行四边形,求![]() 的面积
的面积![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,当![]() 的面积为24时,是否存在这样的点
的面积为24时,是否存在这样的点![]() ,使
,使![]() 为正方形?若存在,求出
为正方形?若存在,求出![]() 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.
 |
查看习题详情和答案>>
已知: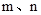 是方程
是方程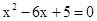 的两个实数根,且
的两个实数根,且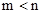 ,抛物线
,抛物线 的图像经过点A(
的图像经过点A(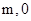 )、B(
)、B(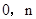 ).
).
(1)求这个抛物线的解析式;
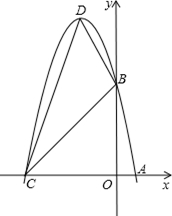
(2) 设(1)中抛物线与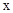 轴的另一交点为C,抛物线的顶点为D,
轴的另一交点为C,抛物线的顶点为D,
试求出点C、D的坐标和△BCD的面积;
(3) P是线段OC上的一点,过点P作PH⊥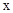 轴,与抛物线交于H点,
轴,与抛物线交于H点,
若直线BC把△PCH分成面积之比为2:3的两部分,请求出P点的坐标.
已知: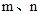 是方程
是方程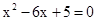 的两个实数根,且
的两个实数根,且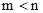 ,抛物线
,抛物线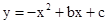 的图像经过点A(
的图像经过点A(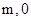 )、B(
)、B(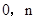 ).
).

(1)求这个抛物线的解析式;
(2) 设(1)中抛物线与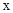 轴的另一交点为C,抛物线的顶点为D,
轴的另一交点为C,抛物线的顶点为D,
试求出点C、D的坐标和△BCD的面积;
(3) P是线段OC上的一点,过点P作PH⊥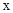 轴,与抛物线交于H点,
轴,与抛物线交于H点,
若直线BC把△PCH分成面积之比为2:3的两部分,请求出P点的坐标.
查看习题详情和答案>>
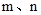 是方程
是方程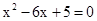 的两个实数根,且
的两个实数根,且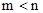 ,抛物线
,抛物线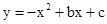 的图像经过点A(
的图像经过点A(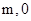 )、B(
)、B(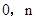 ).
).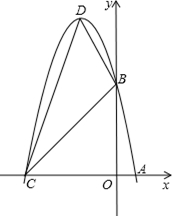
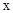 轴的另一交点为C,抛物线的顶点为D,
轴的另一交点为C,抛物线的顶点为D,