0 45362 45370 45376 45380 45386 45388 45392 45398 45400 45406 45412 45416 45418 45422 45428 45430 45436 45440 45442 45446 45448 45452 45454 45456 45457 45458 45460 45461 45462 45464 45466 45470 45472 45476 45478 45482 45488 45490 45496 45500 45502 45506 45512 45518 45520 45526 45530 45532 45538 45542 45548 45556 447348
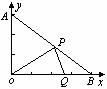 (1)用含t的代数式表示点P的坐标;
(1)用含t的代数式表示点P的坐标;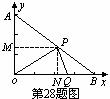 ∵PM∥x轴,∴
∵PM∥x轴,∴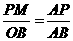 .∴
.∴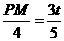 .∴PM=
.∴PM=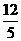 t.
t. 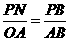 .∴
.∴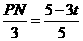 .∴PN=3-
.∴PN=3-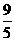 t.
t.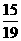 .
. 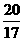 .
. 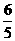 ),Q(3,0),O(0,0).设抛物线的解析式为y=a(x-3)(x-0),即y=a(x2-3x).将P(
),Q(3,0),O(0,0).设抛物线的解析式为y=a(x-3)(x-0),即y=a(x2-3x).将P(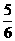 .∴y=-
.∴y=-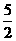 x.
x. 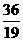 ,
,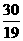 ),Q(
),Q(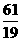 ,0),O(0,0).求得抛物线的解析式为y=-
,0),O(0,0).求得抛物线的解析式为y=-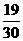 x2+
x2+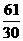 x,相应给分.
x,相应给分.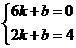 ,
,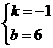 ,
,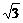 +m(O<m≤1)的图象为直线
+m(O<m≤1)的图象为直线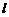 ,直线
,直线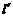 ,△ABC三个顶点的坐标分别为A(-
,△ABC三个顶点的坐标分别为A(-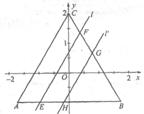
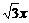 +2 y=
+2 y=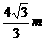 0<m≤1 0<s≤
0<m≤1 0<s≤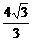
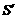 ,则
,则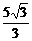
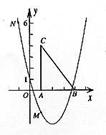
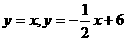 的图象交于点A。动点P从点O开始沿OA方向以每秒1个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设它与△OAB重叠部分的面积为S.
的图象交于点A。动点P从点O开始沿OA方向以每秒1个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设它与△OAB重叠部分的面积为S.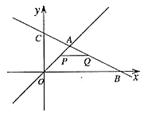 解:(1)由
解:(1)由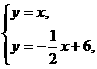 可得
可得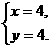
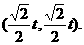
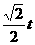 ,并且点Q在
,并且点Q在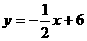 上。
上。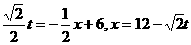 ,
,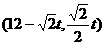 。
。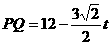 。
。
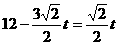 时,
时,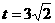 。
。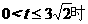 ,
,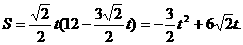
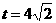 ,
,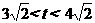 时,
时,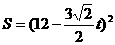
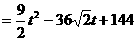 。
。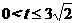 中,
中,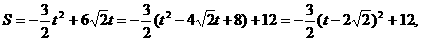
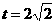 时,S的最大值为12.
时,S的最大值为12. 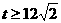 .
.  如图,二资助函数
如图,二资助函数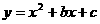 的图象经过点M(1,-2)、N(-1,6).
的图象经过点M(1,-2)、N(-1,6).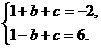 解得
解得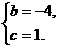
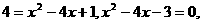
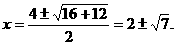
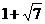 个单位.
个单位.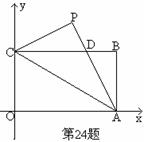 已知如图,矩形OABC的长OA=
已知如图,矩形OABC的长OA=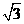 ,宽OC=1,将△AOC沿AC翻折得△APC。
,宽OC=1,将△AOC沿AC翻折得△APC。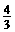 x2+bx+c上,求b,c的值,并说明点C在此抛物线上;
x2+bx+c上,求b,c的值,并说明点C在此抛物线上;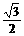 ,
,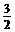 );
);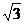 ,0)在抛物线上,故 -
,0)在抛物线上,故 -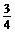 +b×
+b×
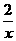 和y=kx+l(k≠O).
和y=kx+l(k≠O).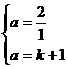 ∴
∴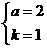
 代人y=kx+l,消去y.得kx2+x一2=0.
代人y=kx+l,消去y.得kx2+x一2=0.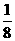
 如图9,抛物线y=ax2+8ax+12a与
如图9,抛物线y=ax2+8ax+12a与 轴交于A、B两点(点A在点B的左侧),抛物线上另有一点
轴交于A、B两点(点A在点B的左侧),抛物线上另有一点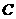 在第一象限,满足∠ ACB为直角,且恰使△OCA∽△OBC.
在第一象限,满足∠ ACB为直角,且恰使△OCA∽△OBC.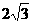 ;(2)
;(2)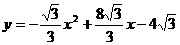 ;(3)4个点:
;(3)4个点: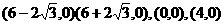
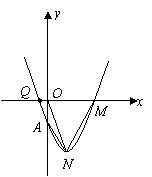 已知抛物线
已知抛物线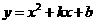 经过点
经过点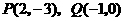 .
. ,与
,与 轴交点为
轴交点为 .求
.求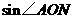 的值.
的值. ,求四边形
,求四边形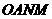 的面积.
的面积.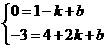
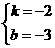 ,
,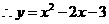 .
. 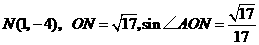 .
. 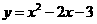 中,令
中,令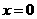 得
得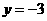 ,
,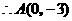 ,
,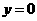 得
得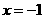 或
或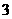 ,
,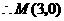 .
. 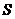 四边形
四边形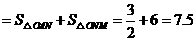 (面积单位)
(面积单位)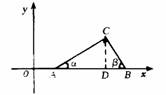
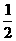 ,x2=2.
,x2=2.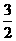 .
.
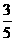 .∴ AD=
.∴ AD=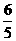 .
.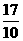 ,
,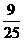 ≠
≠