0 45364 45372 45378 45382 45388 45390 45394 45400 45402 45408 45414 45418 45420 45424 45430 45432 45438 45442 45444 45448 45450 45454 45456 45458 45459 45460 45462 45463 45464 45466 45468 45472 45474 45478 45480 45484 45490 45492 45498 45502 45504 45508 45514 45520 45522 45528 45532 45534 45540 45544 45550 45558 447348
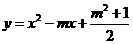 与
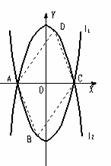
与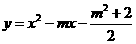 ,这两个二次函数的图象中的一条与x轴交于A, B两个不同的点.
,这两个二次函数的图象中的一条与x轴交于A, B两个不同的点.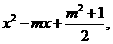
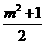 =-m2-2<0,
=-m2-2<0,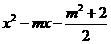 .
.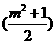 =-m2-2<0,
=-m2-2<0,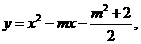
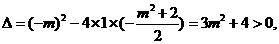
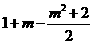 =0.
=0.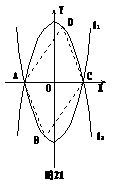
 如图10(单位:m),等腰三角形ABC以2米/秒的速度沿直线L向正方形移动,直到AB与CD重合。设x秒时,三角形与正方形重叠部分的面积为y
如图10(单位:m),等腰三角形ABC以2米/秒的速度沿直线L向正方形移动,直到AB与CD重合。设x秒时,三角形与正方形重叠部分的面积为y .
. :
: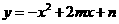 (
( ,
,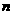 为常数,且
为常数,且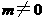 ,
,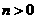 )的顶点为
)的顶点为 ,与
,与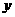 轴交于点
轴交于点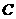 ;抛物线
;抛物线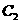 与抛物线
与抛物线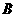 ,连接
,连接 ,
,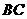 ,
,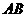 .
.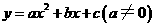 的顶点坐标为
的顶点坐标为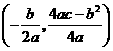 .
.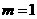 时,判定
时,判定 的形状,并说明理由;
的形状,并说明理由;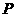 ,使得四边形
,使得四边形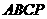 为菱形?如果存在,请求出
为菱形?如果存在,请求出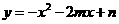 .
.  点
点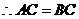 .
. 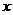 轴于
轴于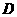 ,过点
,过点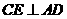 于
于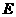 .
. 当
当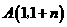 ,
,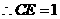 .
.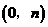 ,
,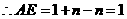 .
.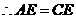 .
.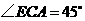 ,
,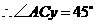 .
. ,
,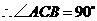 .
. 为等腰直角三角形.
为等腰直角三角形. 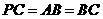 .
.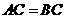 ,
,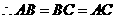 .
.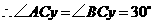 .
.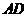 对称.
对称.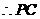 与
与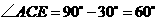 .
.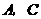 的坐标分别为
的坐标分别为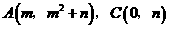 ,
,
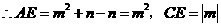 .
.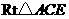 中,
中,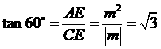 .
.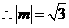 ,
,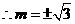 .
.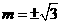 .
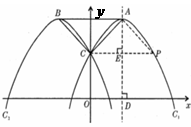
.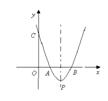 (1)求抛物线的表达式及P点的坐标;
(1)求抛物线的表达式及P点的坐标;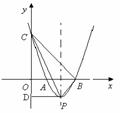 又∵抛物线与x轴交于A(m,0)、B(n,0)两点,
又∵抛物线与x轴交于A(m,0)、B(n,0)两点,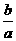 ,mn=
,mn=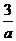 ,
,
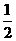 ×3×3+
×3×3+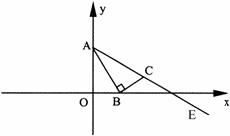 (2)当点B在x轴上运动时,设点C的纵、横坐标分别为y、x,试求y与x的函数关系式(当点B运动到O点时,点C也与O点重合);
(2)当点B在x轴上运动时,设点C的纵、横坐标分别为y、x,试求y与x的函数关系式(当点B运动到O点时,点C也与O点重合);
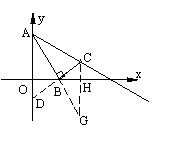 ∵∠OAB=∠BAC,∠AOB=∠ABC=Rt∠ ,∴△ABO∽△ABC ,∴
∵∠OAB=∠BAC,∠AOB=∠ABC=Rt∠ ,∴△ABO∽△ABC ,∴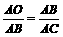 ,由此可求得:AC=
,由此可求得:AC=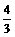

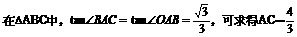
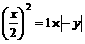
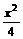 ,当O、B、C三点重合时,y=x=0,∴y与x的函数关系式为:y=
,当O、B、C三点重合时,y=x=0,∴y与x的函数关系式为:y=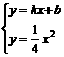 ,消去y得:x2-4kx-4b=0,则有
,消去y得:x2-4kx-4b=0,则有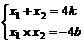 ,由题设知:
,由题设知: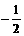 ,当k1=2、b=-1时,
,当k1=2、b=-1时,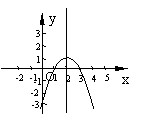 (3)由题意列方程组得:
(3)由题意列方程组得: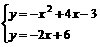
 已知抛物线
已知抛物线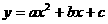 与y
与y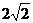
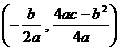 在直线CM上,所以
在直线CM上,所以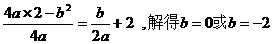
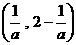
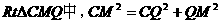
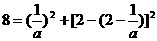 ,解得,
,解得,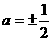 。
。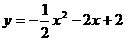 或
或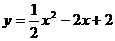 以下同下。
以下同下。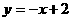 上,∴
上,∴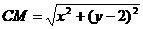 ,∵
,∵
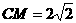
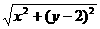 =
=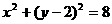
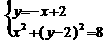 得
得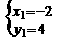
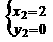
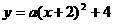 ,∵抛物线过(0,2)点,
,∵抛物线过(0,2)点,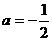 ,∴
,∴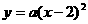
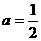 ,∴
,∴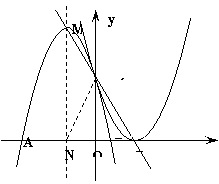 ∴所求抛物线为:
∴所求抛物线为: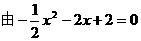 ,得
,得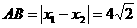
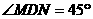 ,作NG⊥CM于G,在
,作NG⊥CM于G,在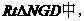
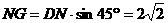 = r
= r 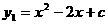 的部分图象如图1所示。
的部分图象如图1所示。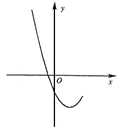
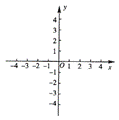
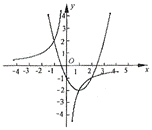
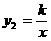 的图象经过(2)中抛物线上点(1,a),试在图2所示直角坐标系中,画出该反比例函数及(2)中抛物线的图象,并利用图象比较
的图象经过(2)中抛物线上点(1,a),试在图2所示直角坐标系中,画出该反比例函数及(2)中抛物线的图象,并利用图象比较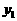 与
与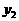 的大小.22. 解:(1)根据图象可知
的大小.22. 解:(1)根据图象可知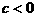
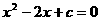 有两个不等的实数根。
有两个不等的实数根。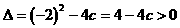 ,且
,且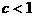
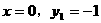 代入
代入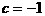
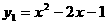
 把
把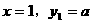 代入
代入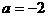
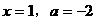 代入
代入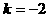
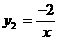
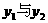 除交点(1,-2)外,还有两个交点大致为
除交点(1,-2)外,还有两个交点大致为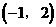 和
和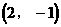
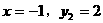 和
和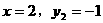 分别代入
分别代入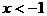 或
或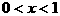 或
或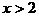 时,
时,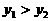
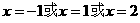 时,
时,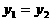
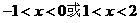 时,
时,