0 447018 447026 447032 447036 447042 447044 447048 447054 447056 447062 447068 447072 447074 447078 447084 447086 447092 447096 447098 447102 447104 447108 447110 447112 447113 447114 447116 447117 447118 447120 447122 447126 447128 447132 447134 447138 447144 447146 447152 447156 447158 447162 447168 447174 447176 447182 447186 447188 447194 447198 447204 447212 447348
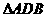 和
和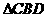 都是等腰直角三角形,且它们所在的平面互相垂直,
都是等腰直角三角形,且它们所在的平面互相垂直,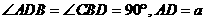
 与
与 所在平面成
所在平面成 角;
角;
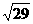 ,设这条最短路线与C1C的交点为N。求
,设这条最短路线与C1C的交点为N。求 平面NMP和平面ABC所成二面角(锐角)的大小(用反三角函数表示)
平面NMP和平面ABC所成二面角(锐角)的大小(用反三角函数表示)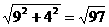
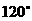 使其与侧面AC1在同一平面上,点P运动到点P1的位置,连接MP1,则MP1就是由点P沿棱柱侧面经过CC1到点M的最短路线。
使其与侧面AC1在同一平面上,点P运动到点P1的位置,连接MP1,则MP1就是由点P沿棱柱侧面经过CC1到点M的最短路线。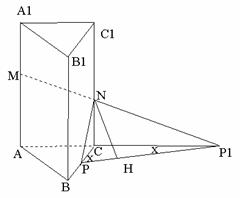 设PC=
设PC=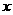 ,则P1C=
,则P1C=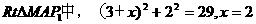
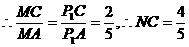
 于H,又CC1
于H,又CC1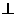 平面ABC,连结CH,由三垂线定理得,
平面ABC,连结CH,由三垂线定理得,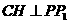 。
。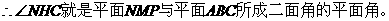
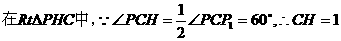
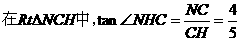
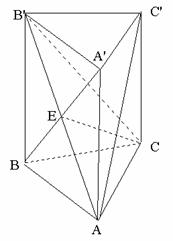 (江安中学)如图在三棱柱ABC-
(江安中学)如图在三棱柱ABC-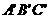 中,已知底面ABC是底角等于
中,已知底面ABC是底角等于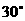 ,底边AC=
,底边AC=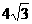 的等腰三角形,且
的等腰三角形,且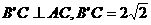 ,面
,面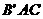 与面ABC成
与面ABC成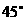 ,
,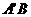 与
与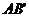 交于点E。
交于点E。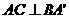 ;
;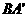 的距离;
的距离;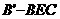 的体积。
的体积。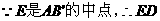 //
//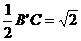
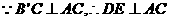
 是底角等于
是底角等于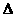 ,
,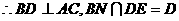
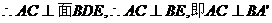

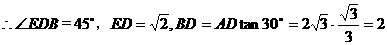
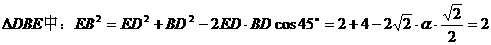
 是异面直线AC与
是异面直线AC与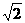

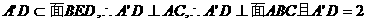
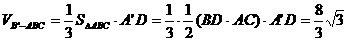
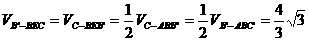
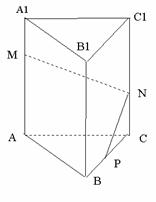 误解:求体积,不考虑用等积法,有时,硬算导致最后错解。
误解:求体积,不考虑用等积法,有时,硬算导致最后错解。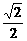 a,∴BMC周长为2x
a,∴BMC周长为2x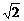 )a,且棱长为b,∴S侧=(1+
)a,且棱长为b,∴S侧=(1+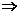 ∠AA1在底面ABC上的射影是∠BAC的平分线”不给出论证。
∠AA1在底面ABC上的射影是∠BAC的平分线”不给出论证。 是边长为4的正方形
是边长为4的正方形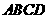 的中心,点
的中心,点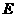 ,
,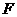 分别是
分别是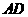 ,
,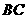 的中点.沿对角线
的中点.沿对角线 把正方形
把正方形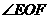 的大小;
的大小;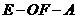 的大小.
的大小.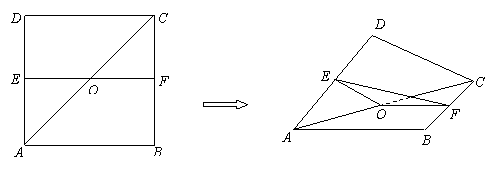 解法一:(Ⅰ)如图,过点E作EG⊥AC,垂足为G,过点F作FH⊥AC,垂足为H,则
解法一:(Ⅰ)如图,过点E作EG⊥AC,垂足为G,过点F作FH⊥AC,垂足为H,则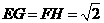 ,
,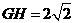 .
.
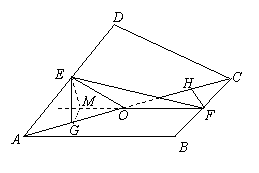
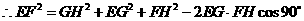
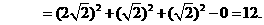
 中,
中,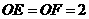 ,
,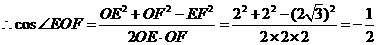 .
. 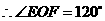 .
.  就是二面角
就是二面角 ,
,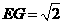 ,
,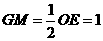 ,
,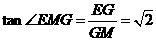 .∴
.∴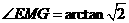 .
.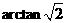 .
.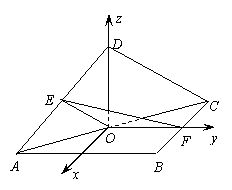 解法二:(Ⅰ)建立如图所示的直角坐标系O-xyz,
解法二:(Ⅰ)建立如图所示的直角坐标系O-xyz, 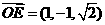 ,
,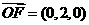 .
.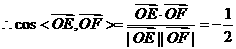 .
.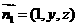 .
.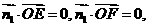 得
得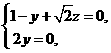 解得
解得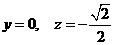 .
.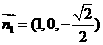 .
.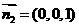 ,
, 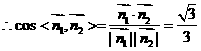 .∴
.∴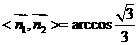 .
. 所以,二面角
所以,二面角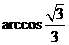 .
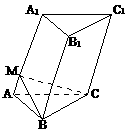
. (石庄中学)如图,在长方体ABCD-A1B1C1D1中,AB=5,AD=8,AA1=4,M为B1C1上一点,且B1M=2,点N在线段A1D上,A1D⊥AN,求: (1)
(石庄中学)如图,在长方体ABCD-A1B1C1D1中,AB=5,AD=8,AA1=4,M为B1C1上一点,且B1M=2,点N在线段A1D上,A1D⊥AN,求: (1) 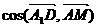 ;
;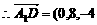 )
) 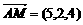
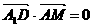 ∴
∴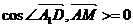
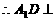 平面AMN,垂足为N.
平面AMN,垂足为N.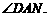
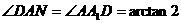
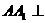 平面ABCD,A1N
平面ABCD,A1N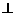 平面AMN,
平面AMN,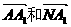 分别成为平面ABCD和平面AMN的法向量。
分别成为平面ABCD和平面AMN的法向量。 ,则
,则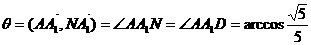
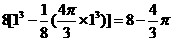 ,除此之外,在以正方体的棱为一条棱的12个
,除此之外,在以正方体的棱为一条棱的12个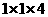 的正四棱柱空间内,小球不能到达的空间共为
的正四棱柱空间内,小球不能到达的空间共为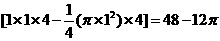 。其他空间小球均能到达。故小球不能到达的空间体积为:
。其他空间小球均能到达。故小球不能到达的空间体积为: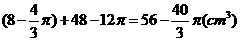 。
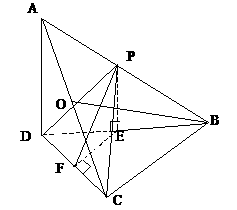
。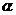 外一点P引平面的三条相等的斜线段,斜足分别为ABC,O为⊿ABC的外心,求证:
外一点P引平面的三条相等的斜线段,斜足分别为ABC,O为⊿ABC的外心,求证: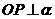 。
。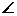 POA=
POA=