摘要:4.点是边长为4的正方形的中心.点.分别是.的中点.沿对角线把正方形折成直二面角D-AC-B. (Ⅰ)求的大小, (Ⅱ)求二面角的大小. 解法一:(Ⅰ)如图.过点E作EG⊥AC.垂足为G.过点F作FH⊥AC.垂足为H.则.. 因为二面角D-AC-B为直二面角. 又在中.. . . (Ⅱ)过点G作GM垂直于FO的延长线于点M.连EM. ∵二面角D-AC-B为直二面角.∴平面DAC⊥平面BAC.交线为AC.又∵EG⊥AC.∴EG⊥平面BAC.∵GM⊥OF.由三垂线定理.得EM⊥OF. ∴就是二面角的平面角. 在RtEGM中.... ∴.∴. 所以.二面角的大小为. 解法二:(Ⅰ)建立如图所示的直角坐标系O-xyz. 则.. . . (Ⅱ)设平面OEF的法向量为. 由得 解得. 所以.. 又因为平面AOF的法向量为. .∴. 所以.二面角的大小为.
网址:http://m.1010jiajiao.com/timu3_id_4471156[举报]
 如图是一幅招贴画的示意图,其中ABCD是边长为2a的正方形,周围是四个全等的弓形.已知O为正方形的中心,G为AD的中点,点P在直线OG上,弧AD是以P为圆心、PA为半径的圆的一部分,OG的延长线交弧AD于点H.设弧AD的长为l,∠APH=θ,θ∈(
如图是一幅招贴画的示意图,其中ABCD是边长为2a的正方形,周围是四个全等的弓形.已知O为正方形的中心,G为AD的中点,点P在直线OG上,弧AD是以P为圆心、PA为半径的圆的一部分,OG的延长线交弧AD于点H.设弧AD的长为l,∠APH=θ,θ∈(| π |
| 4 |
| 3π |
| 4 |
| OP |
| l |
| π |
| 4 |
 (2013•枣庄二模)如图所示,墙上挂有边长为2的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为1的圆孤,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则它击中阴影部分的概率是
(2013•枣庄二模)如图所示,墙上挂有边长为2的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为1的圆孤,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则它击中阴影部分的概率是1-
| π |
| 4 |
1-
.| π |
| 4 |
 (2013•枣庄二模)如图所示,墙上挂有一块边长为2的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为1的扇形.某人向此木板投镖,假设每次都能击中木板,且击中阴影部分的概率为
(2013•枣庄二模)如图所示,墙上挂有一块边长为2的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为1的扇形.某人向此木板投镖,假设每次都能击中木板,且击中阴影部分的概率为1-
| π |
| 4 |
1-
.| π |
| 4 |
 是边长为
是边长为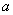 的正方形,以
的正方形,以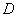 为圆心,
为圆心,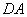 为半径的圆弧与以
为半径的圆弧与以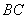 为直径的
为直径的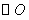 交于点
交于点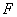 ,延长
,延长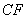 交
交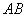 于
于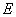 .(1)求证:
.(1)求证: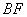 的长.
的长.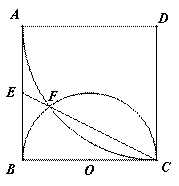
 ,若矩阵
,若矩阵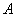 属于特征值3的一个特征向量为
属于特征值3的一个特征向量为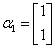 ,属于特征值-1的一个特征向量为
,属于特征值-1的一个特征向量为 ,求矩阵
,求矩阵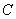 的极坐标方程为
的极坐标方程为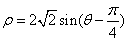 ,以极点为原点,极轴为
,以极点为原点,极轴为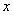 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线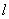 的参数方程为
的参数方程为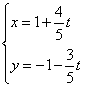 (
(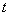 为参数),求直线
为参数),求直线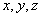 满足
满足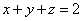 ,求
,求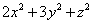 的最小值;
的最小值;