0 447031 447039 447045 447049 447055 447057 447061 447067 447069 447075 447081 447085 447087 447091 447097 447099 447105 447109 447111 447115 447117 447121 447123 447125 447126 447127 447129 447130 447131 447133 447135 447139 447141 447145 447147 447151 447157 447159 447165 447169 447171 447175 447181 447187 447189 447195 447199 447201 447207 447211 447217 447225 447348
 则
则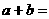 ( )
( )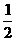 B.a>1 C.a<
B.a>1 C.a<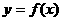 的图象是曲线C,则曲线C与直线
的图象是曲线C,则曲线C与直线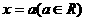 ( )
( )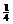 ,b =
,b =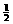 C.a=0,b=1或a=
C.a=0,b=1或a=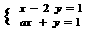 有唯一解
有唯一解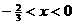
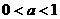 ,给出下列四个不等式:
,给出下列四个不等式: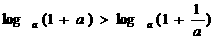 ;②
;②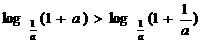 ;
;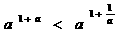 ; ④
; ④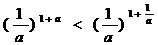 。
。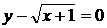 ,x、y
,x、y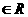 },N={y|
},N={y|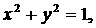 x、y
x、y N等于( )
N等于( ) B.
R C. M D. N
B.
R C. M D. N [解](1)h(x)= (-2x+3)(x-2) x∈[1,+∞)
[解](1)h(x)= (-2x+3)(x-2) x∈[1,+∞)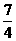 )2+
)2+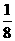
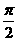
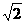 sinx, α=π,
sinx, α=π,