0 447047 447055 447061 447065 447071 447073 447077 447083 447085 447091 447097 447101 447103 447107 447113 447115 447121 447125 447127 447131 447133 447137 447139 447141 447142 447143 447145 447146 447147 447149 447151 447155 447157 447161 447163 447167 447173 447175 447181 447185 447187 447191 447197 447203 447205 447211 447215 447217 447223 447227 447233 447241 447348
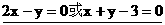 ; 15.
; 15. 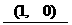 ;
;  .
.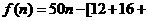 …
…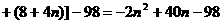 .
. ,得
,得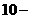
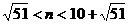 .
.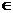 N,故n=3,4,5,…,17.∴ 当n=3时,即第3年开始获利.
N,故n=3,4,5,…,17.∴ 当n=3时,即第3年开始获利.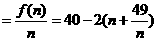 .
.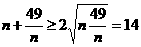 ,当且仅当n=7时取“=”号.
,当且仅当n=7时取“=”号.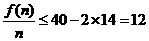 (万元).
(万元).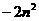 +40n-98=-2
+40n-98=-2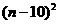 +102.
+102.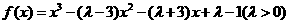 在区间[n,m]上为减函数,记m的最大值为m0,n的最小值为n 0,且有m0- n 0=4.
在区间[n,m]上为减函数,记m的最大值为m0,n的最小值为n 0,且有m0- n 0=4.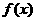 的解析式;
的解析式;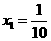 ,公差
,公差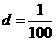 .又过点
.又过点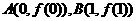 的直线方程为
的直线方程为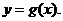 试问:在数列{xn}中,哪些项满足
试问:在数列{xn}中,哪些项满足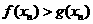 ?
?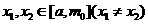 ,都有
,都有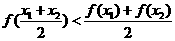 成立,求a的最小值.
成立,求a的最小值.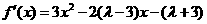 由题意可知
由题意可知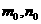 为方程
为方程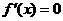 的两根
的两根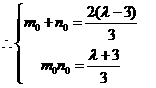 其中
其中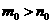
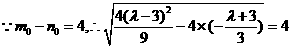
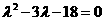 解得
解得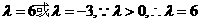
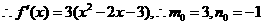
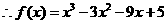
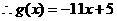 6/
6/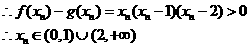
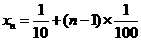 可解得
可解得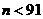 或
或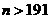
 当
当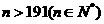 时,满足题意 (3)
时,满足题意 (3)
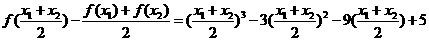
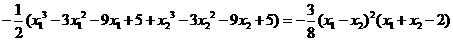 由题意,
由题意,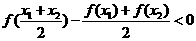 恒成立,即
恒成立,即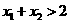 恒成立
恒成立 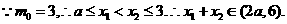
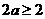 成立,即只要
成立,即只要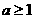 成立
成立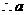 的最小值为1
的最小值为1
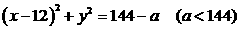 可知圆心M的坐标为(12,0),
依题意:
可知圆心M的坐标为(12,0),
依题意:  ,
, 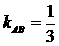 ,
, 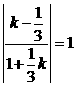 ,解得:
,解得: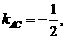
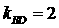 (2分)
(2分) 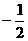 ,
,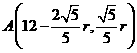 ,
,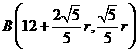 …………(6分)
…………(6分)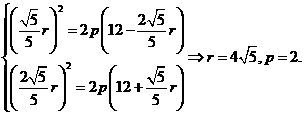
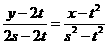
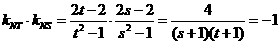
 平面EBD;
平面EBD;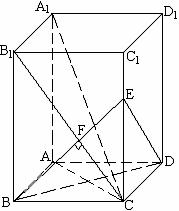 又BD
又BD BE=B, ∴A1C⊥平面EBD. ……(4分)
BE=B, ∴A1C⊥平面EBD. ……(4分) 平面A1B1C,AB
平面A1B1C,AB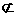 平面A1B1C,
平面A1B1C, 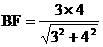
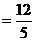 ,
, 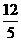 .……(8分)
.……(8分)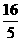 , CF=
, CF=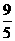 , EF=
, EF=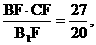 EC=
EC=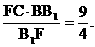
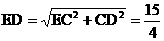 ,……(11分)
,……(11分)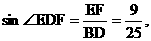 即ED与平面A1B1C所成角为
即ED与平面A1B1C所成角为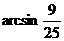 .……(12分)
.……(12分)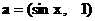 ,
, 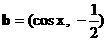 .
.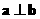 时, 求
时, 求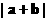 的值; (2) 求函数
的值; (2) 求函数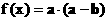 的值域.
的值域.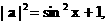
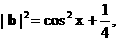
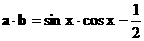 …… (3分)
…… (3分)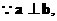 ∴
∴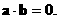 ……(4分) 又
……(4分) 又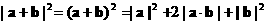
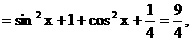 ∴
∴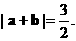 ……(7分)
……(7分)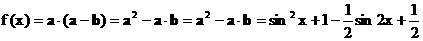 ……(8分)
……(8分)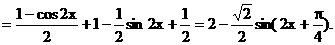 ……(10分)
……(10分)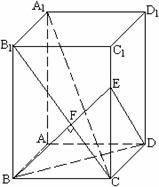 ∴
∴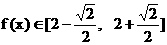 .……(12分)
.……(12分)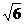 , 则半球
, 则半球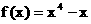 在点P处的切线平行于直线
在点P处的切线平行于直线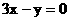 , 则点P的坐标为
.
, 则点P的坐标为
.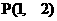 且在坐标轴上截距相等的直线方程为
.
且在坐标轴上截距相等的直线方程为
.