3．如图.在长方体ABCD-A1B1C1D1中.AB=5.AD=8.AA1=4.M为B1C1上一点.且B1M=2.点N在线段A1D上.A1D⊥AN.求: (1) , (2) 直线AD与平面ANM——青夏教育精英家教网——

摘要：3．如图.在长方体ABCD-A1B1C1D1中.AB=5.AD=8.AA1=4.M为B1C1上一点.且B1M=2.点N在线段A1D上.A1D⊥AN.求: (1) , (2) 直线AD与平面ANM所成的角的大小, (3) 平面ANM与平面ABCD所成角的大小. 解:(1) 以A为原点.AB.AD.AA1所在直线为x轴.y轴.z轴. 则D.A1 ) ∵ ∴ 知A1D⊥AM.又由已知A1D⊥AN.平面AMN.垂足为N. 因此AD与平面所成的角即是易知 (3) ∵平面ABCD.A1N平面AMN. ∴分别成为平面ABCD和平面AMN的法向量. 设平面AMN与平面ABCD所成的角为.则

网址：http://m.1010jiajiao.com/timu3_id_4471155[举报]

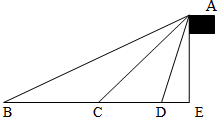高一某班研究性小组成员为了测量永嘉中学旗杆高度收集了如下数据：（如图）在B点测得∠ABE=θ，前进30米至C点处，测得∠ACE=2θ，再继续前进10

米至点D处，测得∠ADE=4θ，则θ的大小为

，旗杆AE的高度为

查看习题详情和答案>>

（08年黄冈中学三模）如图，在直三棱柱ABC―A₁B₁C₁中， .

（Ⅰ）若D为AA₁中点，求证：平面B₁CD平面B₁C₁D；

（Ⅱ）若二面角B₁―DC―C₁的大小为60°，求AD的长.

查看习题详情和答案>>

（08年长郡中学二模文）如图，在△ABC中，角A、B、C的对边分别为、、c,

且8=7，，AB边上的高CM长为.

(Ⅰ)求的值； (Ⅱ)求△ABC的面积

查看习题详情和答案>>

（08年扬州中学）如图，在四棱锥P―ABC中，PA⊥底面ABCD，∠DAB=90°，AB∥CD，AD=CD=2AB=2，E、F分别为PC、CD的中点

⑴证明：CD⊥平面BEF；

⑵设PA=k?AB，且AD与PC所成的角为60°，求k的值．

查看习题详情和答案>>

（08年雅礼中学二模文）如图，在底面是菱形的四棱锥P―ABCD中，，点E在PD上，且PE：ED=2：1

(Ⅰ)证明：PA⊥平面ABCD；

(Ⅱ)求二面角P―AC―E的大小．

查看习题详情和答案>>