20.本小题主要考查相互独立事件和互斥事件有一个发生的概率的计算方法,考查运用概率
知识解决实际问题的能力. 满分12分.
(Ⅰ)解:因为甲坑内的3粒种子都不发芽的概率为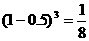 ,所以甲坑不需要补
,所以甲坑不需要补
种的概率为 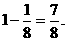
3个坑都不需要补种的概率
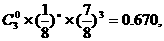
恰有1个坑需要补种的概率为

恰有2个坑需要补种的概率为
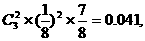
3个坑都需要补种的概率为
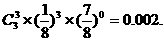
补种费用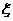 的分布为
的分布为
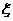 |
0 |
10 |
20 |
30 |
|
P |
0.670 |
0.287 |
0.041 |
0.002 |
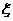 的数学期望为
的数学期望为
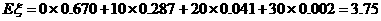
 求导数:
求导数: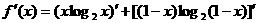

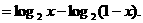
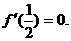
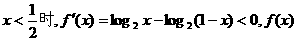 在区间
在区间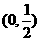 是减函数,
是减函数,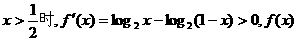 在区间
在区间 是增函数.
是增函数.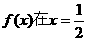 时取得最小值,
时取得最小值,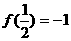 ,
, 时命题成立,即若正数
时命题成立,即若正数 ,
,
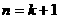 时,若正数
时,若正数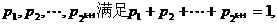
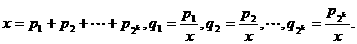
 为正数,且
为正数,且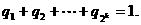
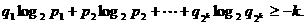
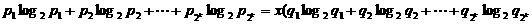
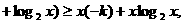 ①
①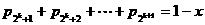 可得
可得
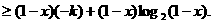 ②
②
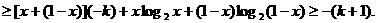
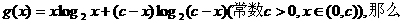

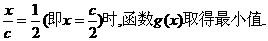
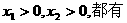
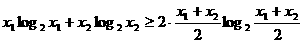
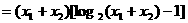 . ①
. ①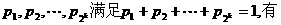
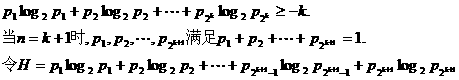


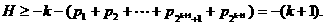
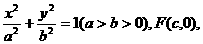
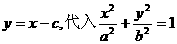
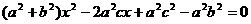 .
.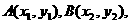
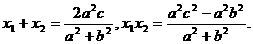
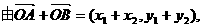
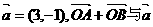 共线,得
共线,得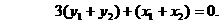

 ,所以椭圆
,所以椭圆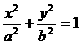 可化为
可化为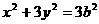 .
.

 在椭圆上,
在椭圆上,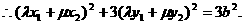
 ①
①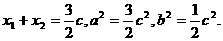
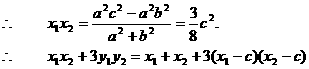
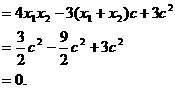
 又,代入①得
又,代入①得 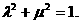
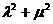 为定值,定值为1.
为定值,定值为1.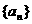 是等比数列,
是等比数列,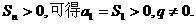

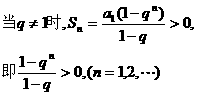
 ①
① ②
②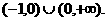
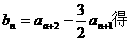
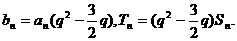
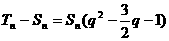
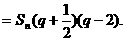
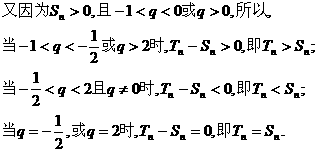
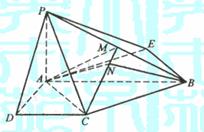 方案一:
方案一: 面PCD,∴面PAD⊥面PCD.
面PCD,∴面PAD⊥面PCD. ,又AB=2,
,又AB=2,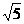 ,
, 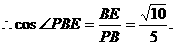

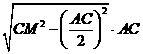 ,
,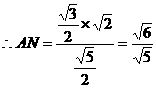 . ∴AB=2,
. ∴AB=2,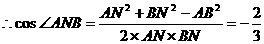
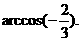
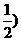 .
.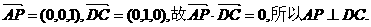
 (Ⅱ)解:因
(Ⅱ)解:因
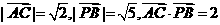 ,
,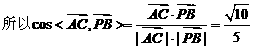 .
.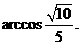
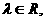 使
使
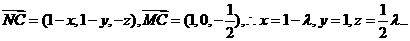
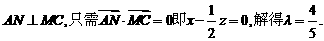
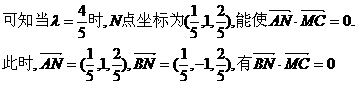
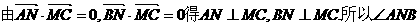 为所求二面角的平面角.
为所求二面角的平面角.
 的图像的对称轴,
的图像的对称轴,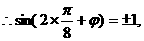

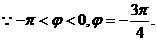



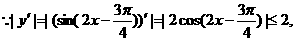
 的切线斜率取值范围为[-2,2],而直线
的切线斜率取值范围为[-2,2],而直线 的斜率为
的斜率为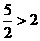 ,所以直线
,所以直线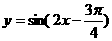 的图像不相切.
的图像不相切. 图像的一条对称轴是直线
图像的一条对称轴是直线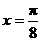 .
.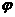 ;
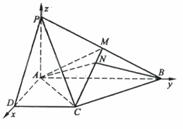
;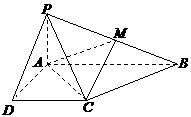 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,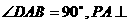 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=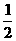 AB=1,M是PB的中点.
AB=1,M是PB的中点.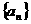 的公比为
的公比为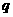 ,前n项和
,前n项和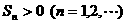 .
.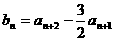 ,记
,记 的前n项和为
的前n项和为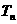 ,试比较
,试比较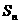 与
与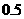 ,若一个坑内至少有1粒种子发芽,则这个坑不需要补种,若一个坑内的种子都没发芽,则这个坑需要补种.假定每个坑至多补种一次,每补种1个坑需10元,用ξ表示补种费用,写出ξ的分布列并求ξ的数学期望.(精确到
,若一个坑内至少有1粒种子发芽,则这个坑不需要补种,若一个坑内的种子都没发芽,则这个坑需要补种.假定每个坑至多补种一次,每补种1个坑需10元,用ξ表示补种费用,写出ξ的分布列并求ξ的数学期望.(精确到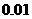 )
) 轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,
轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,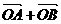 与
与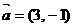 共线.
共线.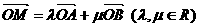 ,证明
,证明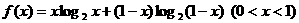 ,求
,求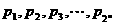 满足
满足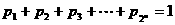 ,证明:
,证明: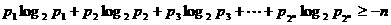
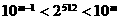 ,则m = 155 .
,则m = 155 .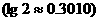
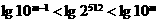 ,即
,即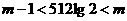 ,
,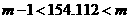 ,即
,即 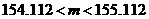 ,∴
,∴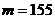 .
.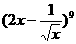 的展开式中,常数项为 672 .(用数字作答)
的展开式中,常数项为 672 .(用数字作答)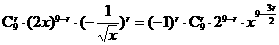 ,令
,令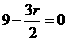 得,
得,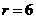 ,∴常数项为
,∴常数项为
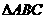 的外接圆的圆心为O,两条边上的高的交点为H,
的外接圆的圆心为O,两条边上的高的交点为H,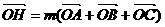 ,则实数
,则实数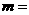 .
.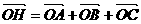 ,∴
,∴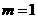 .(但当
.(但当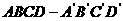 中,过对角线
中,过对角线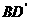 的一个平面交
的一个平面交 于E,交
于E,交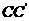 于F,则
于F,则

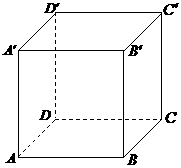 ①四边形
①四边形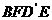 一定是平行四边形
一定是平行四边形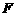
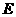
 ④四边形
④四边形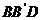
 以上结论正确的为
.(写出所有正确结论的编号)
以上结论正确的为
.(写出所有正确结论的编号)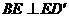 ,又
,又 ,
,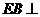 平面
平面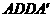 ,产生矛盾;
,产生矛盾;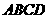 ;
;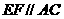 ,又
,又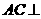 平面
平面 ( )
( )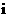 (B)
(B)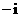 (C)
(C) (D)
(D)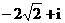
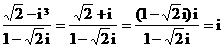 ,故选A.
,故选A. 为全集,
为全集,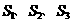 是
是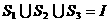 ,则下面论断正确的是( )
,则下面论断正确的是( ) (A)
(A)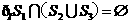 (B)
(B)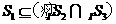
 (D)
(D)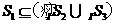
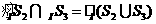 所表示的部分是图中蓝色
所表示的部分是图中蓝色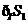 所表示的部分是图中除去
所表示的部分是图中除去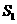 的部分,
的部分,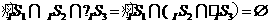 ,故选C.
,故选C.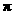 ,则球的表面积为 ( )
,则球的表面积为 ( )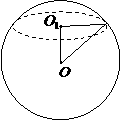 (A)
(A)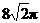 (B)
(B)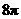 (C)
(C)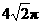 (D)
(D)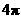
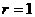 ,
,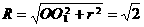 ,
,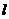 过点
过点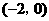 ,当直线
,当直线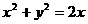 有两个交点时,其斜率k的取值范围是( )
有两个交点时,其斜率k的取值范围是( )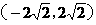 (B)
(B)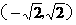
 (D)
(D)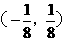
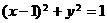 ,
,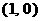 ,半径
,半径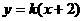 ,即
,即 ,设直线
,设直线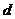 ,则
,则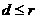 ,
,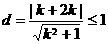 ,∴
,∴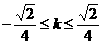 .故选C.
.故选C.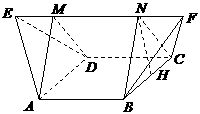 (5)如图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且
(5)如图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且 均为正三角形,EF∥AB,EF=2,则该多面体的体积为( )
均为正三角形,EF∥AB,EF=2,则该多面体的体积为( )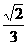 (B)
(B)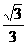
 (D)
(D)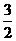

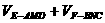 ,∵
,∵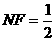 ,
,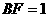 ,∴
,∴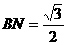 ,作NH垂直于点H,则H为BC的中点,则
,作NH垂直于点H,则H为BC的中点,则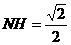 ,∴
,∴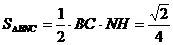 ,∴
,∴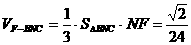 ,
,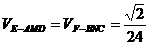 ,
,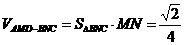 ,∴
,∴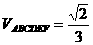 ,故选A.
,故选A.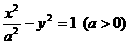 的一条准线与抛物线
的一条准线与抛物线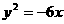 的准线重合,则该双曲线的离心率为( )
的准线重合,则该双曲线的离心率为( )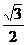 (B)
(B)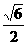 (D)
(D)
 ,∴
,∴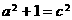 ,抛物线
,抛物线 ,因为双曲线
,因为双曲线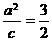 ,解得
,解得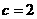 ,所以
,所以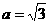 ,所以离心率为
,所以离心率为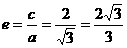 ,故选D.
,故选D.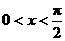 时,函数
时,函数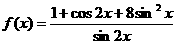 的最小值为( )
的最小值为( )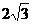 (C)4 (D)
(C)4 (D)
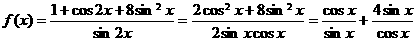
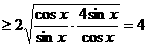 ,当且仅当
,当且仅当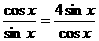 ,即
,即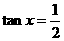 时,取“
时,取“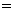 ”,∵
”,∵ ,故选.
,故选.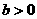 ,二次函数
,二次函数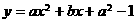 的图像为下列之一
的图像为下列之一

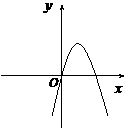
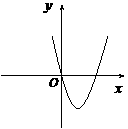
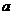 的值为( )
的值为( )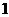 (B)
(B)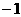 (C)
(C)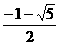 (D)
(D)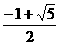
 ,故其对称轴为
,故其对称轴为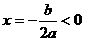 ,所以也不符合;只有第三个图可以,由图象过原点,得
,所以也不符合;只有第三个图可以,由图象过原点,得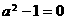 ,开口向下,所以
,开口向下,所以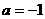 ,故选B.
,故选B.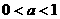 ,函数
,函数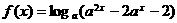 ,则使
,则使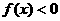 的
的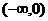 (B)
(B)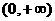 (C)
(C)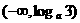 (D)
(D)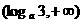
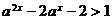 ,解得
,解得  或
或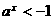 (舍去),
(舍去),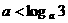 ,故选C.
,故选C.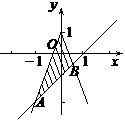 (10)在坐标平面上,不等式组
(10)在坐标平面上,不等式组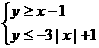 所表示的平面区域的面积为( )
所表示的平面区域的面积为( )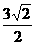 (D)2
(D)2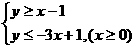 或
或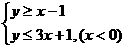 ,
,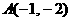 ,
,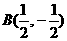 , ∴
, ∴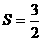 ,故选B.
,故选B.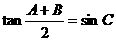 ,给出以下四个论断:
,给出以下四个论断: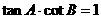 ②
②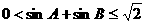
 ④
④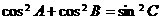
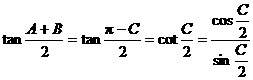 ,
,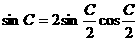 ,
,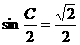 ,∴
,∴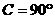 ,
,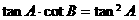 ,∴①不一定成立,
,∴①不一定成立,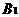 ∵
∵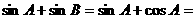
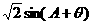 ,∴
,∴

 ∵
∵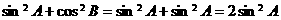 ,∴③不一定成立,
,∴③不一定成立, ∵
∵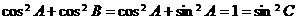 ,∴④成立,故选B.
,∴④成立,故选B.


 [点拨]考查三角公式的灵活运用.
[点拨]考查三角公式的灵活运用.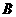 [解析]解法一:(直接法)
[解析]解法一:(直接法)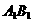 、
、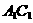 、
、 成异面直线的有15对;
成异面直线的有15对; 、
、 、
、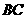 成异面直线的有9对(除去与上底面的);
成异面直线的有9对(除去与上底面的);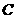
 ③与侧棱
③与侧棱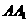 、
、 、
、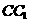 成异面直线的有6对(除去与上下底面的);
成异面直线的有6对(除去与上下底面的);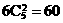 对;
对;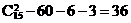 对.
对.