(17)(本小题13分)


(18)(本小题13分)
解:(1)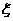 的所有可能值为0,1,2,3,4,5。
的所有可能值为0,1,2,3,4,5。
由等可能性事件的概率公式得
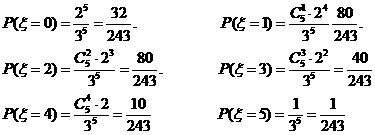
从而,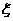 的分布列为
的分布列为
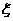 |
0 |
1 |
2 |
3 |
4 |
5 |
 |
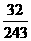 |
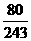 |
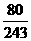 |
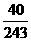 |
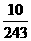 |
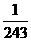 |
(II)由(I)得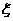 的期望为
的期望为
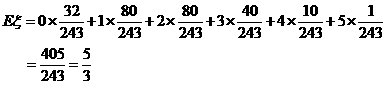
(19)(本小题13分)
(I)证:由已知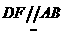 且
且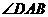 为直角。故ABFD是矩形。从而
为直角。故ABFD是矩形。从而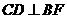 。又
。又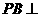 底面ABCD,
底面ABCD,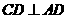 ,故由三垂线定理知
,故由三垂线定理知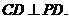 D
D 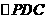 中,E、F分别为PC、CD的中点,故EF//PD,从而
中,E、F分别为PC、CD的中点,故EF//PD,从而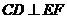 ,由此得
,由此得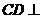 面BEF。
面BEF。
(II)连接AC交BF于G,易知G为AC的中点,连接EG,则在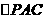 中易知EG//PA。又因PA
中易知EG//PA。又因PA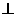 底面ABCD,故EG
底面ABCD,故EG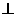 底面ABCD。在底面ABCD中,过G作GH
底面ABCD。在底面ABCD中,过G作GH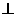 BD。垂足为H,连接EH,由三垂线定理知EH
BD。垂足为H,连接EH,由三垂线定理知EH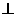 BD。从而
BD。从而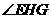 为二面角E-BD-C的平面角。
为二面角E-BD-C的平面角。
设
以下计算GH,考虑底面的平面图(如答(19)图2)。连结GD,因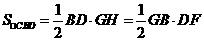
故GH=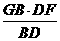 .在
.在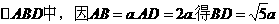 。而
。而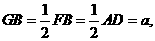
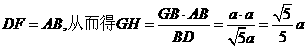 。因此,
。因此,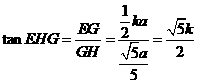 。由
。由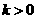 知
知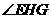 是锐角。故要使
是锐角。故要使 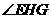
 ,必须
,必须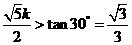 ,解之得,中的取值范围为
,解之得,中的取值范围为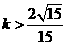
(20)(本小题13分)
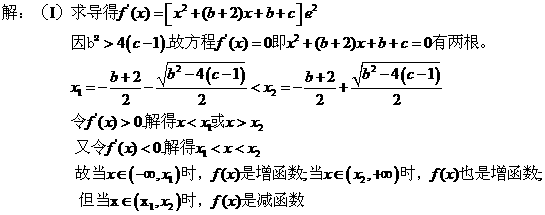
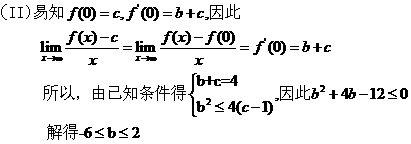
(21)题(本小题12分)

(22)(本小题12分)
证:(I)由题设及椭圆的几何性质有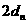
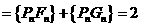 ,故
,故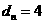 。设
。设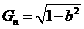 ,则右准线方程为
,则右准线方程为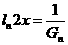 .因此,由题意
.因此,由题意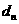 应满足
应满足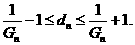 即
即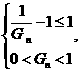 解之得:
解之得: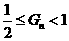 。即
。即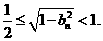 从而对任意
从而对任意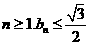
(II)高点 的坐标为
的坐标为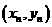 ,则由
,则由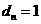 及椭圆方程易知
及椭圆方程易知
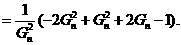 因
因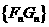
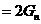 ,故
,故
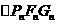 的面积为
的面积为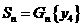 ,从而
,从而 。令
。令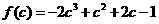 。由
。由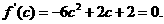 得两根
得两根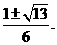 从而易知函数
从而易知函数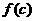 在
在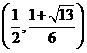 内是增函数。而在
内是增函数。而在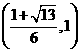 内是减函数。
内是减函数。
现在由题设取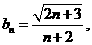 则
则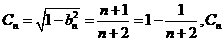 是增数列。又易知
是增数列。又易知
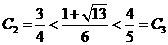 。故由前已证,知
。故由前已证,知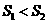 ,且
,且
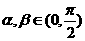 ,
,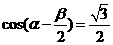 ,
,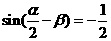 ,则
,则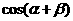 的值等于
的值等于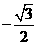 (B)
(B)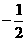 (C)
(C)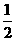 (D)
(D)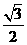
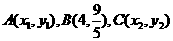 是右焦点为
是右焦点为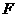 的椭圆
的椭圆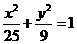 上三个不同的点,则“
上三个不同的点,则“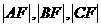 成等差数列”是“
成等差数列”是“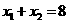 ”的
”的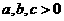 且
且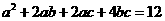 ,则
,则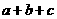 的最小值是
的最小值是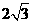 (B)3 (C)2 (D)
(B)3 (C)2 (D)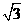
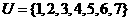 ,
,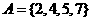 ,
,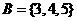 ,则
,则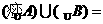
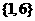 (B)
(B)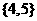 (C)
(C) (D)
(D)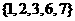
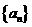 中,若
中,若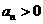 且
且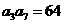 ,
,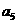 的值为
的值为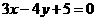 相切的圆的方程为
相切的圆的方程为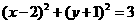 (B)
(B)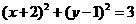
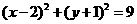 (D)
(D)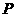 是平面
是平面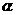 外一点,则下列命题正确的是
外一点,则下列命题正确的是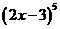 的展开式中
的展开式中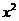 的系数为
的系数为 的反函数为
的反函数为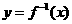 ,且
,且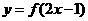 的图像过点
的图像过点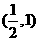 ,则
,则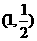 (C)
(C)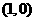 (D)
(D)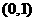
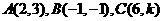 ,其中
,其中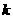 为常数。若
为常数。若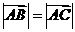 ,则
,则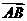 与
与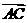 的夹角为
的夹角为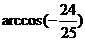 (B)
(B)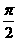 或
或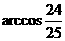

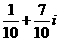 (12)
(12)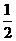 (13)
(13)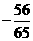 (14)
(14)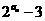
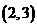 (16)
(16)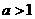
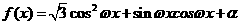 (其中
(其中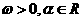 ),且
),且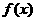 的图象在
的图象在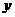 轴右侧的第一个最高点的横坐标为
轴右侧的第一个最高点的横坐标为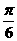 。
。 的值。
的值。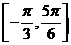 上的最小值为
上的最小值为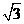 ,求
,求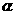 的值。
的值。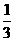 ,用
,用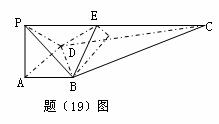 如图,在四棱锥
如图,在四棱锥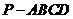 中,
中,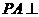 底面ABCD,
底面ABCD,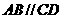 ,
,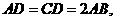 E、F分别为
E、F分别为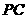 、
、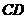 中点。
中点。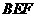 ;
;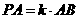 ,且二面角
,且二面角 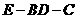 的平面角大小
的平面角大小 ,求
,求 的取值范围。
的取值范围。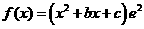 ,其中
,其中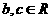 为常数。
为常数。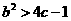 ,讨论函数
,讨论函数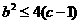 ,且
,且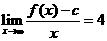 ,试证:
,试证: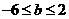
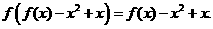
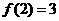 ,求
,求 ;又若
;又若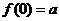 ,求
,求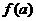 ;
;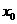 ,使得
,使得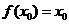 ,求函数
,求函数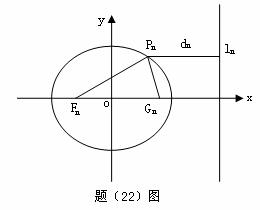 已知一列椭圆
已知一列椭圆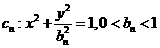 。
。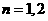 ……。若椭圆
……。若椭圆 上有一点
上有一点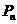 ,使
,使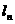 的距离
的距离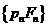 与
与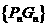 的等差中项,其中
的等差中项,其中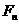 、
、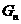 分别是
分别是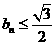
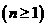 ;
;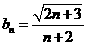 ,并用
,并用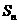 表示
表示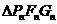 的面积,试证:
的面积,试证: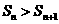
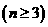
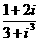 的值是
。
的值是
。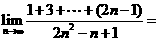 。
。 则
则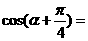 。
。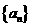 中,若
中,若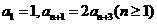 ,则该数列的通项
,则该数列的通项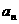
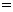 。
。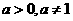 ,函数
,函数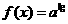 有最大值,则不等式
有最大值,则不等式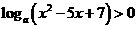 的解集为
。
的解集为
。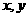 满足约束条件
满足约束条件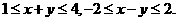 若目标函数
若目标函数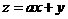 (其中
(其中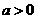 )仅在点
)仅在点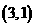 处取得最大值,则
处取得最大值,则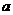 的取值范围为
。
的取值范围为
。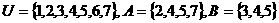 ,则
,则 =
=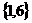 (B)
(B) (C)
(C)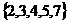 (D)
(D)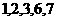
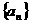 中,若
中,若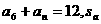 是数列的
是数列的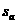 的值为( )
的值为( )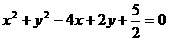 相切的直线方程为( )
相切的直线方程为( )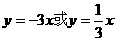 (B)
(B)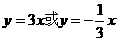
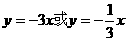 (D)
(D)
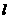 与平面
与平面 ,使
,使 的展开式中各项系数之和为64,则展开式的常数项为( )
的展开式中各项系数之和为64,则展开式的常数项为( )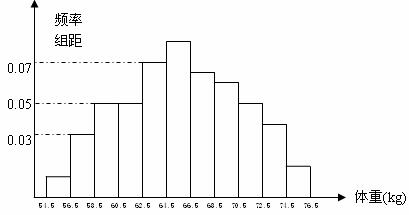
 的学生人数是( )
的学生人数是( )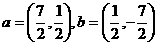 的夹角相等,且模为1的微量是( )
的夹角相等,且模为1的微量是( )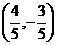 (B)
(B)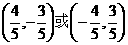
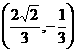 (D)
(D)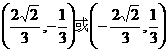
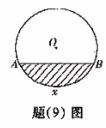 (9)如图所示,单位圆中
(9)如图所示,单位圆中 的长为
的长为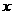 ,
,
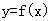 的图像是( )
的图像是( )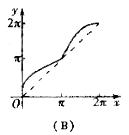
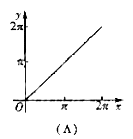
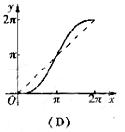
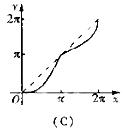
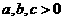 且
且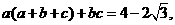 则
则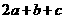 的最小值为( )
的最小值为( )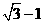 (B)
(B)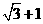 (C)
(C)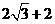 (D)
(D)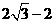
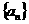 的首项
的首项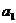 =4,前n项和为Sn ,且
=4,前n项和为Sn ,且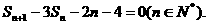
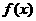 =
=

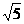 )且方向向量为
)且方向向量为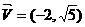 的直线l交椭圆C于A、 B两点,交x轴于M点,又
的直线l交椭圆C于A、 B两点,交x轴于M点,又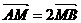

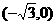 ,右顶点为(2,0).
,右顶点为(2,0).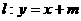 与椭圆C有两个不同的交点A和B,且
与椭圆C有两个不同的交点A和B,且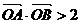 (其中O为原点), 求实数m的取值范围.
(其中O为原点), 求实数m的取值范围.