(1)已知 ,函数
,函数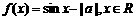 为奇函数,则a=
为奇函数,则a=
(A)0 (B)1 (C)-1 (D)±1
解:法一:由函数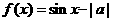 是定义域为R的奇函数,则
是定义域为R的奇函数,则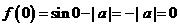 , 即
, 即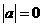 ,则a=0,选A
,则a=0,选A
法二: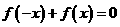 得:
得: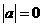 ,则a=0,选A
,则a=0,选A
点评:主要考查奇函数的定义和性质
(2)圆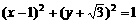 的切线方程中有一个是
的切线方程中有一个是
(A)x-y=0 (B)x+y=0 (C)x=0 (D)y=0
解:圆心为(1, ),半径为1,故此圆必与y轴(x=0)相切,选C
),半径为1,故此圆必与y轴(x=0)相切,选C
点评:本题主要考查圆的定义及直线与圆的位置关系
(3)某人5次上班途中所花的时间(单位:分钟)分别为x,y,10,11,9.已知这组数据的平均数为10,方差为2,则|x-y|的值为
(A)1 (B)2 (C)3 (D)4
解: 由平均数公式为10,得 则
则 ;又由于方差为2,则
;又由于方差为2,则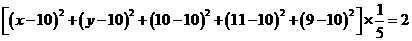 得
得 ,所以有
,所以有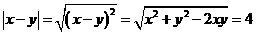 ,故选(D)
,故选(D)
点评:本题主要考查平均数与方差的定义等统计方面的基础知识
(4)为了得到函数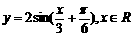 的图像,只需把函数
的图像,只需把函数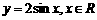 的图像上所有的点
的图像上所有的点
(A)向左平移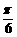 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 倍(纵坐标不变)
倍(纵坐标不变)
(B)向右平移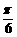 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 倍(纵坐标不变)
倍(纵坐标不变)
(C)向左平移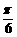 个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
(D)向右平移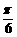 个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
解:根据三角函数的图像变换法则易得:把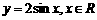 向左平移
向左平移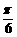 个单位长度得
个单位长度得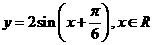 ,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)故选(C)
,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)故选(C)
点评:本题主要考查形如 的三角函数图像的变换
的三角函数图像的变换
(5) 的展开式中含x的正整数指数幂的项数是
的展开式中含x的正整数指数幂的项数是
(A)0 (B)2 (C)4 (D)6
解:展开式通项为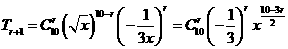 ,若展开式中含x的正整数指数幂,即
,若展开式中含x的正整数指数幂,即 所以
所以 ,选(B)
,选(B)
点评:本题主要考查二项式定理的相关知识
(6)已知两点M(-2,0)、N(2,0),点P为坐标平面内的动点,满足 =0,则动点P(x,y)的轨迹方程为
=0,则动点P(x,y)的轨迹方程为
(A)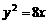 (B)
(B) (C)
(C)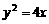 (D)
(D)
解:由题意 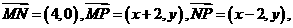

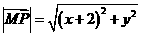 ,所以有
,所以有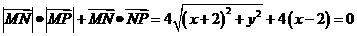
即: ,故选(B)
,故选(B)
点评:本题主要考查点的轨迹方程的求法
(7)若A、B、C为三个集合,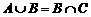 ,则一定有
,则一定有
(A)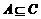 (B)
(B)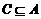 (C)
(C)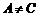 (D)
(D)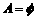
解:由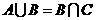 知,
知, ,故选(A)
,故选(A)
点评:本题主要考查集合间关系的运算
(8)设a、b、c是互不相等的正数,则下列等式中不恒成立的是
(A)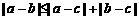 (B)
(B)
(C)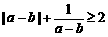 (D)
(D)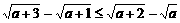
解:因为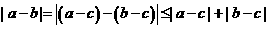 ,所以(A)恒成立;
,所以(A)恒成立;
在(B)两侧同时乘以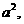 得
得
 所以(B)恒成立;
所以(B)恒成立;
(C)中,当a>b时,恒成立,a<b时,不成立;
(D)中,分子有理化得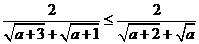 恒成立,故选(C)
恒成立,故选(C)
点评:本题主要考查不等式的相关知识
|
|
|
|
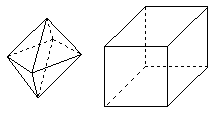 (9)两相同的正四棱锥组成如图1所示的几何体,可放棱长为1的正方体内,使正四棱锥的底面ABCD与正方体的某一个平面平行,且各顶点均在正方体的面上,则这样的几何体体积的可能值有
(9)两相同的正四棱锥组成如图1所示的几何体,可放棱长为1的正方体内,使正四棱锥的底面ABCD与正方体的某一个平面平行,且各顶点均在正方体的面上,则这样的几何体体积的可能值有
|
(C)3个 (D)无穷多个
解:法一:本题可以转化为一个正方形可以有多少个内接正方形,显然有无穷多个
法二:通过计算,显然两个正四棱锥的高均为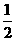 ,考查放入正方体后,面ABCD所在的截面,显然其面积是不固定的,取值范围是
,考查放入正方体后,面ABCD所在的截面,显然其面积是不固定的,取值范围是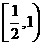 ,所以该几何体的体积取值范围是
,所以该几何体的体积取值范围是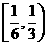
点评:本题主要考查学生能否迅速构造出一些常见的几何模型,并不是以计算为主
 (10)右图中有一个信号源和五个接收器。接收器与信号源在同一个串联线路中时,就能接收到信号,否则就不能接收到信号。若将图中左端的六个接线点随机地平均分成三组,将右端的六个接线点也随机地平均分成三组,再把所有六组中每组的两个接线点用导线连接,则这五个接收器能同时接收到信号的概率是
(10)右图中有一个信号源和五个接收器。接收器与信号源在同一个串联线路中时,就能接收到信号,否则就不能接收到信号。若将图中左端的六个接线点随机地平均分成三组,将右端的六个接线点也随机地平均分成三组,再把所有六组中每组的两个接线点用导线连接,则这五个接收器能同时接收到信号的概率是
(A) (B)
(B)
(C) (D)
(D)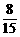
解:由题意,左端的六个接线点随机地平均分成三组有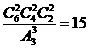 种分法,同理右端的六个接线点也随机地平均分成三组有
种分法,同理右端的六个接线点也随机地平均分成三组有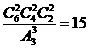 种分法;要五个接收器能同时接收到信号,则需五个接收器与信号源串联在同一个线路中,即五个接收器的一个全排列,再将排列后的第一个元素与信号源左端连接,最后一个元素与信号源右端连接,所以符合条件的连接方式共有
种分法;要五个接收器能同时接收到信号,则需五个接收器与信号源串联在同一个线路中,即五个接收器的一个全排列,再将排列后的第一个元素与信号源左端连接,最后一个元素与信号源右端连接,所以符合条件的连接方式共有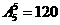 种,所求的概率是
种,所求的概率是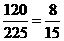 ,故选(D)
,故选(D)
点评:本题要求学生能够熟练运用排列组合知识解决计数问题,并进一步求得概率问题,其中隐含着平均分组问题。
 (本小题满分14分)
(本小题满分14分) 的距离
的距离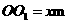 ,则
,则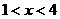 。
。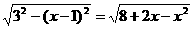 ,(单位:
,(单位: )
) =
=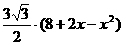 ,(单位:
,(单位: )
)
 (单位:
(单位: )
)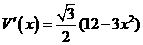 。
。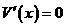 ,解得
,解得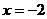 (不合题意,舍去)或
(不合题意,舍去)或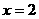 。
。 时,
时, ,
,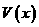 为增函数;
为增函数;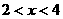 时,
时,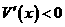 ,
,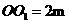 时,帐篷的体积最大,最大体积为
时,帐篷的体积最大,最大体积为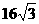
 (-6,0)、
(-6,0)、 (6,0)。
(6,0)。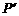 、
、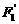 、
、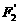 ,求以
,求以 +
+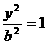
 ,其半焦距
,其半焦距 。
。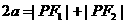
 , ∴
, ∴
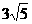 ,
, ,故所求椭圆的标准方程为
,故所求椭圆的标准方程为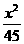 +
+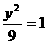 ;
; 、
、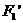 (0,-6)、
(0,-6)、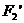 (0,6)
(0,6) -
-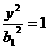
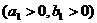 ,由题意知半焦距
,由题意知半焦距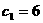 ,
,
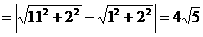 , ∴
, ∴
 ,
,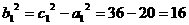 ,故所求双曲线的标准方程为
,故所求双曲线的标准方程为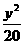 -
- 。
。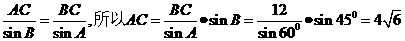
 ,则
,则 的最大值为 ▲
的最大值为 ▲ 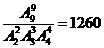
 = ▲
= ▲ 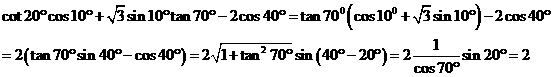
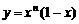 在x=2处的切线与y轴交点的纵坐标为
在x=2处的切线与y轴交点的纵坐标为 ,则数列
,则数列 的前n项和的公式是 ▲
的前n项和的公式是 ▲  ,令x=0,求出切线与y轴交点的纵坐标为
,令x=0,求出切线与y轴交点的纵坐标为 ,所以
,所以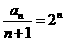 ,则数列
,则数列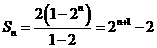
 的解集为 ▲
的解集为 ▲ 
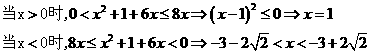
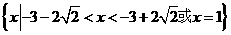
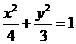 ,抛物线C2:
,抛物线C2: ,且C1、C2的公共弦AB过椭圆C1的右焦点.
,且C1、C2的公共弦AB过椭圆C1的右焦点.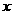 轴时,求
轴时,求 、
、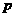 的值,并判断抛物线C2的焦点是否在直线AB上;
的值,并判断抛物线C2的焦点是否在直线AB上; )为0.8,要求洗完后的清洁度是0.99.有两种方案可供选择,方案甲:一次清洗;方案乙:两次清洗.该物体初次清洗后受残留水等因素影响,其质量变为
)为0.8,要求洗完后的清洁度是0.99.有两种方案可供选择,方案甲:一次清洗;方案乙:两次清洗.该物体初次清洗后受残留水等因素影响,其质量变为 (1≤a≤3).设用
(1≤a≤3).设用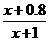 (
(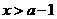 ),用
),用 质量的水第二次清洗后的清洁度是
质量的水第二次清洗后的清洁度是 ,其中
,其中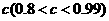 是该物体初次清洗后的清洁度.
是该物体初次清洗后的清洁度. 时方案乙的用水量,并比较哪一种方案用水量较少;
时方案乙的用水量,并比较哪一种方案用水量较少; ,数列{
,数列{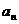 }满足:
}满足:
 ;(ⅱ)
;(ⅱ)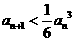 .
. (Ⅲ)求点P到平面QAD的距离.
(Ⅲ)求点P到平面QAD的距离. (Ⅱ)平均有多少家煤矿必须整改;
(Ⅱ)平均有多少家煤矿必须整改;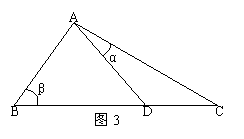 (本小题满分12分)
(本小题满分12分)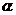 ,∠ABC=
,∠ABC=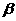 .
. ;
; DC,求
DC,求