20、(2005年梅州市)东海体育用品商场为了推销某一运动服,先做了市场调查,得到数据如下表:
|
卖出价格x(元/件) |
50 |
51 |
52 |
53 |
 …… …… |
|
销售量p(件) |
500 |
490 |
480 |
470 |
…… |
(1)以x作为点的横坐标,p作为纵坐标,把表中的
数据,在图8中的直角坐标系中描出相应的点,观察连结
各点所得的图形,判断p与x的函数关系式;
(2)如果这种运动服的买入件为每件40元,试求销售
利润y(元)与卖出价格x(元/件)的函数关系式
(销售利润=销售收入-买入支出);
(3)在(2)的条件下,当卖出价为多少时,能获得最大利润?
解:(1)p与x成一次函数关系。
设函数关系式为p=kx+b ,则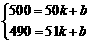
解得:k=-10,b=1000 , ∴ p=-10x+1000
经检验可知:当x=52,p=480,当x=53,p=470时也适合这一关系式
∴所求的函数关系为p=-10x+1000
(2)依题意得:y=px-40p=(-10x+1000)x-40(-10x+1000)
∴ y=-10x2+1400x-40000
(3)由y=-10x2+1400x-40000 可知,当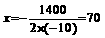 时,y有最大值
时,y有最大值
∴ 卖出价格为70元时,能花得最大利润。
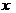 (m),面积为
(m),面积为 (m2),求
(m2),求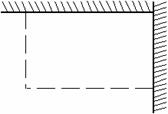
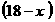

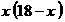
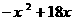
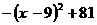
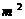
 =-1<0,
=-1<0,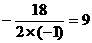 时(0<9<18),
时(0<9<18), 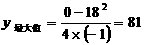 (
(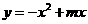 过点A(4,0),O为坐标原点,
过点A(4,0),O为坐标原点,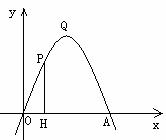 Q是抛物线的顶点. ⑴求
Q是抛物线的顶点. ⑴求 的值;⑵点P是
的值;⑵点P是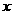 轴上方抛物线上的一个动点,过P作PH⊥
轴上方抛物线上的一个动点,过P作PH⊥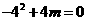 ∴
∴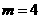 ∴
∴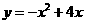
 ⑵设点P的坐标为
⑵设点P的坐标为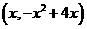
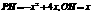

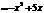
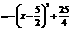 ∴当
∴当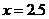 时,折线P-H-O的长度最长为
时,折线P-H-O的长度最长为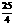 ∵点Q的横坐标为2∴这个同学的说法不正确。
∵点Q的横坐标为2∴这个同学的说法不正确。 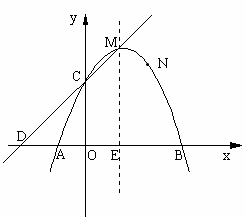 (3)点P在抛物线的对称轴x=1上运动,请探索:在x轴上方是否存在这样的P点,使以P为圆心的圆经过A、B两点,并且与直线CD相切,若存在,请求出点P的坐标;若不存在,请说明理由。
(3)点P在抛物线的对称轴x=1上运动,请探索:在x轴上方是否存在这样的P点,使以P为圆心的圆经过A、B两点,并且与直线CD相切,若存在,请求出点P的坐标;若不存在,请说明理由。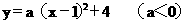
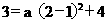 解得a=-1
解得a=-1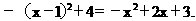
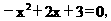 解得:
解得: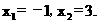
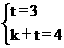 即k=1,t=3
即k=1,t=3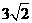
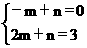 解得m=1,n=1
解得m=1,n=1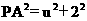
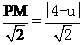
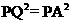 得方程:
得方程: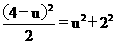 ,解得
,解得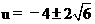 ,
,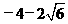 ,符合题意的u=
,符合题意的u=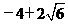 ,
,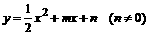 与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴.
与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴.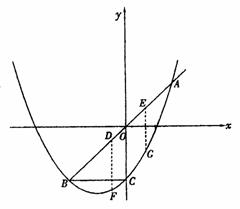 (2)设D、E是线段AB上异于A、B的两个动点(点E在点D的上方),DE=
(2)设D、E是线段AB上异于A、B的两个动点(点E在点D的上方),DE=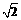 ,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.
,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.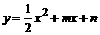 与y轴交于点C
∴C(0,n)
与y轴交于点C
∴C(0,n)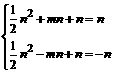 解得:n=0(舍去),n=-2;m=1
解得:n=0(舍去),n=-2;m=1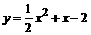
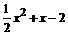 ,G的纵坐标:
,G的纵坐标: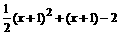
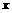 -(
-(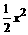 EG=(x+1)- [
EG=(x+1)- [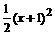
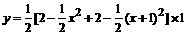
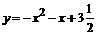
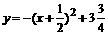
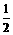 时,y最大值=3
时,y最大值=3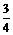 .
.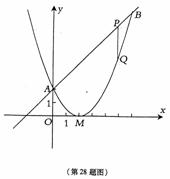 (2005年龙岩市)已知二次函数图象的顶点坐标为M(2,0),直线y=x+2与该二次函数的图象交于A、B两点,其中点A在y轴上(如图示) (1)求该二次函数的解析式; (2)P为线段用上一动点(A、B两端点除外),过P作x轴的垂线与二次函数的图象交于点Q,设线段PQ的长为
(2005年龙岩市)已知二次函数图象的顶点坐标为M(2,0),直线y=x+2与该二次函数的图象交于A、B两点,其中点A在y轴上(如图示) (1)求该二次函数的解析式; (2)P为线段用上一动点(A、B两端点除外),过P作x轴的垂线与二次函数的图象交于点Q,设线段PQ的长为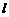 ,点P的横坐标为x,求出
,点P的横坐标为x,求出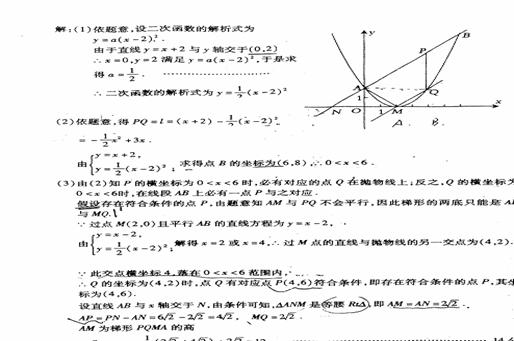
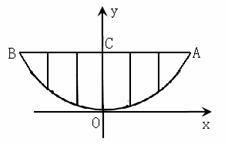 (丽水市2005)某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米.
(丽水市2005)某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米.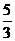 , ∴抛物线的解析式为y=
, ∴抛物线的解析式为y=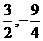 ),对称轴为直线x=
),对称轴为直线x=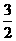
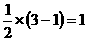
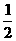 )2+
)2+