43、(2004年河北)光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台.现将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.
两地区与该农机租赁公司商定的每天的租赁价格见下表:
|
|
每台甲型收割机的租金 |
每台乙型收割机的租金 |
|
A地区 |
1800元 |
1600元 |
|
B地区 |
1600元 |
1200元 |
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79600元,说
明有多少种分派方案,并将各种方案设计出来;
(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提
出一条合理建议.
解:(1)若派往A地区的乙型收割机为x台,则派往A地区的甲型收割机为(30-x)台;派往B地区的乙型收割机为(30-x)台,派往B地区的甲型收割机为(x-10)台.
∴y=1600x+1800(30-x)+1200(30-x)+1600(x-10)=200x+74000.
x的取值范围是:10≤x≤30(x是正整数).
(2)由题意得200x+74000≥79600,
解不等式得x≥28.由于10≤x≤30,∴x取28,29,30这三个值,
∴有3种不同分配方案.
① 当x=28时,即派往A地区甲型收割机2台,乙型收割机28台;派往B
地区甲型收割机18台,乙型收割机2台.
② 当x=29时,即派往A地区甲型收割机1台,乙型收割机29台;派往B
地区甲型收割机19台,乙型收割机1台.
③ 当x=30时,即30台乙型收割机全部派往A地区;20台甲型收割机全部派往B地区.
(3)由于一次函数y=200x+74000的值y是随着x的增大而增大的,所以,当x=30时,y取得最大值.如果要使农机租赁公司这50台联合收割机每天获得租金最高,只需x=30,此时,y=6000+74000=80000.
建议农机租赁公司将30台乙型收割机全部派往A地区;20台甲型收割要全部派往B地区,可使公司获得的租金最高.
40、(淮安市2004) 国泰玩具厂工人的工作时间:每月25天,每天8小时.待遇:按件计酬,多劳多得,每月另加福利工资100元,按月结算.该厂生产A、B两种产品,工人每生产一件A种产品,可得报酬0.75元,每生产一件B种产品,可得报酬1.40元.下表记录了工人小李的工作情况:
|
生产A种产品件数(件) |
生产B种产品件数(件) |
总时间(分) |
|
l |
1 |
35 |
|
3 |
2 |
85 |
根据上表提供的信息,请回答下列问题:
(1)小李每生产一件A种产品、每生产一件B种产品,分别需要多少分钟?
(2)如果生产各种产品的数目没有限制,那么小李每月的工资数目在什么范围之内?
解:(1)解:设小李每生产一件A种产品、每生产一件B种产品分别需要x分钟和y
分钟,根据题意,得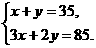 解之,得
解之,得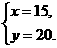
(由记录表直接推出正确结论的,同样给分)
(2)方法一:设小李每月生产A种产品x件,B种产品y件(x、y均为非负整数),月工资
数目为w元, 根据题意,得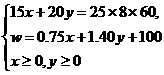 ,即
,即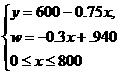
由于- 0.3<0,因此当x=O时,w最大=-O.3·0+940=940
当x=800时,w最小=-O.3·800+940=700.
因为生产各种产品的数目没有限制,所以700≤w≤940.
即小李每月的工资数目不低于700元而不高于940元.
方法二:由(1)知小李生产A种产品每分钟可获利O.05元,生产B种产品每分钟可获利O.07元, 若小李全部生产A种产品,每月的上资数目为700元,若小李全部生产B种产品,每月的工资数目为940元
小李每月的工资数目不低于700元而不高于940元.


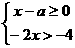 有解,则
有解,则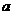 的取值范围为
的取值范围为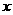 的不等式组
的不等式组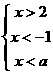 ,无解,则
,无解,则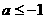 B
B 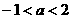 C
C  D
D 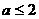
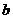 吨的固定流量增加.如果同时开动2台机组需30小时处理完污水,同时开动4台机组需10小时处理完污水.若要求5小时内将污水处理完毕,那么至少要同时开动多少台机组?
吨的固定流量增加.如果同时开动2台机组需30小时处理完污水,同时开动4台机组需10小时处理完污水.若要求5小时内将污水处理完毕,那么至少要同时开动多少台机组?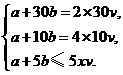 (①②各1分,③2分,其中③写成等式不扣分)… 5分
(①②各1分,③2分,其中③写成等式不扣分)… 5分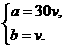 ……………………………………………………………………… 7分
……………………………………………………………………… 7分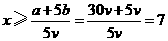 .
.