摘要:某校的围墙上端由一段段相同的凹曲拱形栅栏组成.如图所示.其拱形图形为抛物线的一部分.栅栏的跨径AB间.按相同的间距0.2米用5根立柱加固.拱高OC为0.6米. (1) 以O为原点.OC所在的直线为y轴建立平面直角坐标系.请根据以上的数据.求出抛物线y=ax2的解析式, (2)计算一段栅栏所需立柱的总长度. 解:(1) 由已知:OC=0.6.AC=0.6. 得点A的坐标为. 代入y=ax2.得a=. ∴抛物线的解析式为y=x2. (2)点D1.D2的横坐标分别为0.2.0.4. 代入y=x2.得点D1.D2的纵坐标分别为: y1=×0.22≈0.07.y2=×0.42≈0.27. ∴立柱C1D1=0.6-0.07=0.53.C2D2=0.6-0.27=0.33. 由于抛物线关于y轴对称.栅栏所需立柱的总长度为: 2(C1D1+ C2D2)+OC=2+0.6≈2.3米.
网址:http://m.1010jiajiao.com/timu3_id_440794[举报]
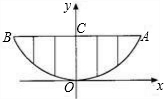 某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米.
某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米.(1)以O为原点,OC所在的直线为y轴建立平面直角坐标系,请根据以上的数据,抛物线y=ax2中a=
(2)计算一段栅栏所需立柱的总长度为
 某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米,以O为原点,OC所在的直线为y轴建立平面直角坐标系,根据以上的数据,则这段栅栏所需立柱的总长度(精确到0.1米)为( )
某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米,以O为原点,OC所在的直线为y轴建立平面直角坐标系,根据以上的数据,则这段栅栏所需立柱的总长度(精确到0.1米)为( )| A、1.5米 | B、1.9米 | C、2.3米 | D、2.5米 |
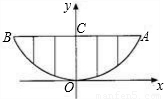 某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米.
某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米.(1)以O为原点,OC所在的直线为y轴建立平面直角坐标系,请根据以上的数据,抛物线y=ax2中a=______;
(2)计算一段栅栏所需立柱的总长度为______米.(精确到0.1米)
查看习题详情和答案>>
 某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米.
某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米. 某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米.
某校的围墙上端由一段段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径AB间,按相同的间距0.2米用5根立柱加固,拱高OC为0.6米.