摘要:如图.已知抛物线与直线y=x交于A.B两点.与y轴交于点C.OA=OB.BC∥x轴. (1)求抛物线的解析式. (2)设D.E是线段AB上异于A.B的两个动点.DE=.过D.E两点分别作y轴的平行线.交抛物线于F.G.若设D点的横坐标为x.四边形DEGF的面积为y.求x与y之间的关系式.写出自变量x的取值范围.并回答x为何值时.y有最大值. (1)∵抛物线与y轴交于点C ∴C(0.n) ∵BC∥x轴 ∴B点的纵坐标为n ∵B.A在y=x上.且OA=OB ∴B ∴ 解得:n=0.n=-2,m=1 ∴所求解析式为: (2)作DH⊥EG于H ∵D.E在直线y=x上 ∴∠EDH=45° ∴DH=EH ∵DE= ∴DH=EH=1 ∵D ∴F的纵坐标:.G的纵坐标: ∴DF=-()=2- EG=(x+1)- []=2- ∴ ∴x的取值范围是-2<x<1 当x=-时.y最大值=3.
网址:http://m.1010jiajiao.com/timu3_id_440797[举报]
如图,已知抛物线![]() 与直线y=2x交于点O(0,0),A(a,12),点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E.
与直线y=2x交于点O(0,0),A(a,12),点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E.

(1)求抛物线的函数解析式;
(2)若点C为OA的中点,求BC的长;
(3)以BC,BE为边构造矩形BCDE,设点D的坐标为(m,n),求出m,n之间的关系式.
如图,已知抛物线 与直线
与直线 交于点O(0,0),
交于点O(0,0),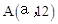 。点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E。
。点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E。

(1)求抛物线的函数解析式;
(2)若点C为OA的中点,求BC的长;
(3)以BC,BE为边构造条形BCDE,设点D的坐标为(m,n),求m,n之间的关系式。
查看习题详情和答案>>
如图,已知抛物线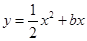 与直线
与直线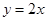 交于点
交于点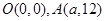 .点
.点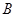 是抛物线上
是抛物线上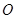 ,
,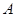 之间的一个动点,过点
之间的一个动点,过点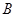 分别作
分别作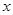 轴、
轴、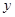 轴的平行线与直线
轴的平行线与直线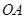 交于点
交于点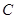 ,
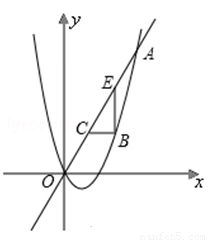
,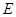 .
.
(1)求抛物线的函数解析式;
(2)若点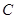 的横坐标为2,求
的横坐标为2,求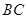 的长;
的长;
(3)以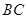 ,
,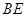 为边构造矩形
为边构造矩形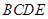 ,设点
,设点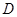 的坐标为
的坐标为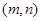 ,求出
,求出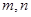 之间的关系式.
之间的关系式.
查看习题详情和答案>>
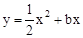 与直线
与直线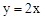 交于点O(0,0),
交于点O(0,0),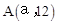 。点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E。
。点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E。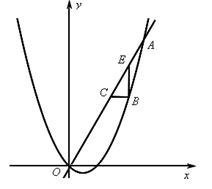
 与直线
与直线 交于点
交于点 .点
.点 是抛物线上
是抛物线上 ,
, 之间的一个动点,过点
之间的一个动点,过点 轴、
轴、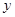 轴的平行线与直线
轴的平行线与直线 交于点
交于点 ,
, .
.
 的长;
的长; 为边构造矩形
为边构造矩形 ,设点
,设点 的坐标为
的坐标为 ,求出
,求出 之间的关系式.
之间的关系式.