0 43984 43992 43998 44002 44008 44010 44014 44020 44022 44028 44034 44038 44040 44044 44050 44052 44058 44062 44064 44068 44070 44074 44076 44078 44079 44080 44082 44083 44084 44086 44088 44092 44094 44098 44100 44104 44110 44112 44118 44122 44124 44128 44134 44140 44142 44148 44152 44154 44160 44164 44170 44178 447348
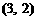 ,那么下列各点在此函数图象上的是( )
,那么下列各点在此函数图象上的是( )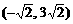 B.
B.
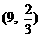 C.
C.
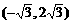 D.
D.
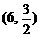
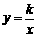 的图象经过点
的图象经过点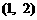 ,则函数
,则函数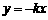 可确定为( )
可确定为( )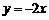 B.
B.
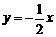 C.
C.
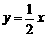 D.
D.
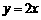
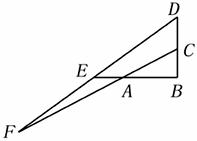
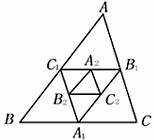
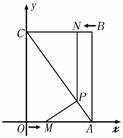
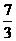 ;(2)易求解析式为y=-x2+4x-3;
;(2)易求解析式为y=-x2+4x-3;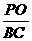 =
=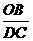 或
或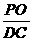 =
=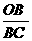 .解得PO=
.解得PO=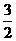 或PO=6.符合题意.∴点P的坐标为(0,6)、(0,-6) 、(0,1.5)、(0,-1.5).
或PO=6.符合题意.∴点P的坐标为(0,6)、(0,-6) 、(0,1.5)、(0,-1.5).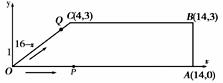
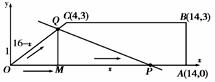
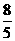 x,
x,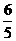 x),当点Q在CB上,坐标为(2x-1,3).
x),当点Q在CB上,坐标为(2x-1,3).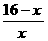 .②当Q在OC上时,作QM⊥OA,垂足为M,则QM=(16-x)×
.②当Q在OC上时,作QM⊥OA,垂足为M,则QM=(16-x)×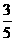 ,∴S△OPQ=
,∴S△OPQ=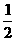 ×
×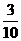 ×(16-x).令
×(16-x).令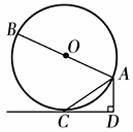
 .
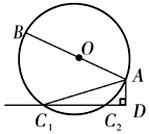
.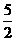 ) ③与x轴的交点坐标(3+
) ③与x轴的交点坐标(3+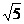 ,0)或(3-
,0)或(3-