摘要:如图.用长为18 m的篱笆.两面靠墙围成矩形的苗圃. (1)设矩形的一边为(m).面积为(m2).求关于的函数关系式.并写出自变量的取值范围, (2)当为何值时.所围苗圃的面积最大.最大面积是多少? 解:(1) 由已知.矩形的另一边长为 则= = 自变量的取值范围是0<<18. (2)∵ == ∴ 当=9时.苗圃的面积最大 最大面积是81 又解: ∵ =-1<0.有最大值. ∴ 当 =时. ()
网址:http://m.1010jiajiao.com/timu3_id_440800[举报]
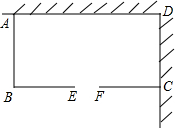 (2011•香坊区模拟)如图,用长为18米的篱笆两面靠墙围成一个矩形苗圃ABCD,其中EF是一个2米宽的门(门不需要篱笆).设边AB的长为x(单位:米),矩形ABCD的面积为S(单位:平方米).
(2011•香坊区模拟)如图,用长为18米的篱笆两面靠墙围成一个矩形苗圃ABCD,其中EF是一个2米宽的门(门不需要篱笆).设边AB的长为x(单位:米),矩形ABCD的面积为S(单位:平方米).(1)求s与x之间的函数关系式(不要求写出自变量的取值范围):
(2)若矩形ABCD的面积为64平方米,且AB<BC,请求出此时AB的长.
 圃. 问矩形苗圃的一边长为多少时面积最大,最大面积是多少?
圃. 问矩形苗圃的一边长为多少时面积最大,最大面积是多少? 圃. 问矩形苗圃的一边长为多少时面积最大,最大面积是多少?
圃. 问矩形苗圃的一边长为多少时面积最大,最大面积是多少?
 (m),面积为
(m),面积为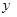 (m2),求
(m2),求 圃. 问矩形苗圃的一边长为多少时面积最大,最大面积是多少?
圃. 问矩形苗圃的一边长为多少时面积最大,最大面积是多少?