4. 某市煤气公司对用户收费方法是:若每月用气量不超过A立方米,只收基本费3元和保险费1元;若用气量超过A立方米时,则超过部分按每立方米B元收超额费,某用户1、2月份煤气用量和付费如下表所示:
|
月份 |
用气量m2 |
煤气费元 |
|
1 |
25 |
14 |
|
2 |
35 |
19 |
(1) 求A、B的值。
(2) 若3月份用煤气32立方米,
则要缴费多少元(煤气费=基本费+超额费+保险费)
25.(1)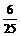 ;(2)
;(2)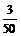 ,
,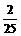 ;(3)班级人数、三好生数、模范生数、成绩提高奖人数;(4)用50个小球,其中3个红球、4个白球、5个黑球,其余均位黄球,把它们装进不透明的口袋中搅均,闭着眼从中摸出一个球,则摸到非黄球的机会就是得到荣誉的机会,摸到红球或白球的机会就是当选为三好生和模范生的机会.
;(3)班级人数、三好生数、模范生数、成绩提高奖人数;(4)用50个小球,其中3个红球、4个白球、5个黑球,其余均位黄球,把它们装进不透明的口袋中搅均,闭着眼从中摸出一个球,则摸到非黄球的机会就是得到荣誉的机会,摸到红球或白球的机会就是当选为三好生和模范生的机会.
某商店举办有奖销售活动,购物满100元者发对奖券一张。在10000张奖券中,设特等奖1个,一等奖10个,二等奖100个。若某人购物刚好满100元,那么他中一等奖的概率是( )
A 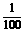 B
B 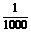 C
C 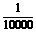 D
D 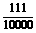
甲、乙、丙三个家电厂家在广告中都声称,他们的某种电子产品在正常情况下的使用寿命都是8年,经质量检测部门对这三家销售的产品的使用寿命进行跟踪调查,统计结果如下:(单位:年)
甲厂:4,5,5,5,5,7,9,12,13,15
乙厂:6,6,8,8,8,9,10,12,14,15
丙厂:4,4,4,6,7,9,13,15,16,16
请回答下面问题:
(1)分别求出以上三组数据的平均数、众数、中位数;
|
|
平均数 |
众数 |
中位数 |
|
甲厂 |
|
|
|
|
乙厂 |
|
|
|
|
丙厂 |
|
|
|
(2)这三个厂家的销售广告分别利用了哪一种表示集中趋势的特征数?
(3)如果你是位顾客,宜选购哪家工厂的产品?为什么?
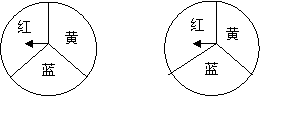
如图所示,每个转盘被分成3个面积相等的扇形,小红和小芳利用它们做游戏:同时自由转动两个转盘,如果两个转盘的指针所停区域的颜色相同,则小红获胜;如果两个转盘的指针所停区域的颜色不相同,则小芳获胜,此游戏对小红和小芳两人公平吗?谁获胜的概率大?
甲、乙两人掷两个普通的正方体骰子,规定掷出“和为7”算甲赢,掷出“和为8”算乙赢,这个游戏是否公平?
A.公平 B.对甲有利 C.对乙有利 D.无法判断
某公司欲聘请一位员工,三位应聘者A、B、C的原始评分如下表
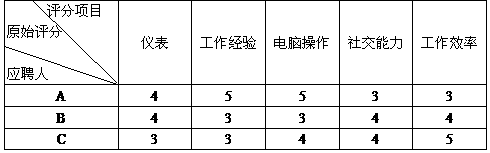
① 如果按五项原始评分的平均数评分,谁将被聘用?② 如果按仪表、工作经验、电脑操作、社交能力、工作效率的原始评分分别占10%、15%、20%、25%、30%综合评分,谁将被聘用?(8分)
某商场设立了一个可以自由转动的转盘(如图),并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品,下表是活动进行中的一组统计数据:
(1) 计算并完成表格:
|
转动转盘的次数n |
100 |
150 |
200 |
500 |
800 |
1000 |
|
落在“铅笔”的次数m |
68 |
111 |
136 |
345 |
546 |
701 |
落在“铅笔”的频率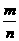 |
|
|
|
|
|
|
(2) 请估计,当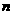 很大时,频率将会接近多少?
很大时,频率将会接近多少?
(3) 假如你去转动该转盘一次,你获得铅笔的概率约是多少?
(4) 在该转盘中,标有“铅笔”区域的扇形的圆心角大约是多少?(精确到1°)(10 分)
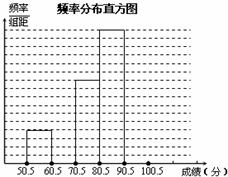
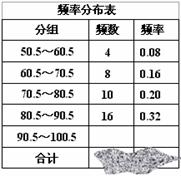
为了让学生了解环保知识,增强环保意识,红星中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题: (1)填充频率分布表中的空格; (2)补全频率分布直方图;
(3)全体参赛学生中,竞赛成绩落在哪组范围内的人数最多?答: 。
(4)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为多少人?答: 。
数学老师对小明在参加中考前的5次数学模拟考试进行统计分析,判断小明的数学成绩是否稳定,于是老师需要知道小明这5次数学成绩的( )
(A)平均数或中位数 (B)方差或极差
(C)众数或频率 (D)频数或众数
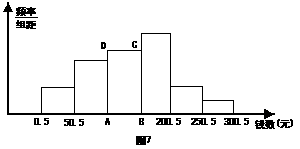
未成年人思想道德建设越来越受到社会的关注。某青少年研究所随机调查了无锡市内某校100名学生寒假中花零花钱的数量(钱数取整数元),以便引导学生树立正确的消费观。根据调查数据制成了频率分布表和频率分布直方图(如图7)。
|
分组 |
频数 |
频率 |
|
0.5~50.5 |
_______ |
0.1 |
|
50.5~______ |
20 |
0.2 |
|
100.5~150.5 |
_______ |
______ |
|
______200.5 |
30 |
0.3 |
|
200.5~250.5 |
10 |
0.1 |
|
250.5~300.5 |
5 |
0.05 |
|
合计 |
100 |
________ |
⑴补全频率分布表;
⑵在频率分布直方图中,长方形ABCD的面积是_________;这次调查的样本容量是_________;
⑶研究所认为,应对消费150元以上的学生提出勤俭节约的建议。试估计应对该校1000名学生中约多少名学生提出这项建议
集市上有一个人在设摊“摸彩”,只见他手拿一个黑色的袋子,内装大小、形状、质量完全相同的白球20只,且每一个球上都写有号码(1-20号)和1只红球,规定:每次只摸一只球。摸前交1元钱且在1--20内写一个号码,摸到红球奖5元,摸到号码数与你写的号码相同奖10元。
(1) 你认为该游戏对“摸彩”者有利吗?说明你的理由。
若一个“摸彩”者多次摸奖后,他平均每次将获利或损失多少元?
某同学进行社会调查,随机抽查了某个地区的20个家庭的收入情况,并绘制了统计图.请你根据统计图给出的信息回答:
(1) 填写完成下表:
|
年收入(万元) |
0.6 |
0.9 |
1.0 |
1.1 |
1.2 |
1.3 |
1.4 |
9.7 |
|
家庭户数 |
|
|
|
|
|
|
|
|
这20个家庭的年平均收入为______万元;
(2) 样本中的中位数是______万元,众数是______万元;
(3) 在平均数、中位数两数中,______更能反映这个地区家庭的年收入水平.
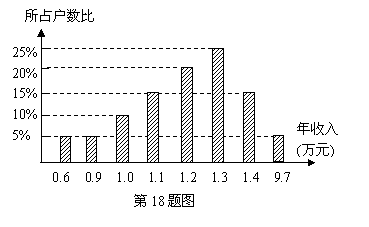
一布袋中有红、黄、白三种颜色的球各一个,它们除颜色外其它都一样。小亮从布袋中摸出一个球后放回去摇匀,再摸出一个球。请你利用列举法(列表或画树状图)分析并求出小亮两次都能摸到白球的概率。
射击集训队在一个月的集训中,对甲、乙两名运动员进行了10次测试,成绩如图所示:
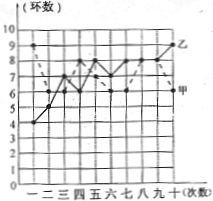 (1)根据右图所提供的信息填写下表:
(1)根据右图所提供的信息填写下表:
|
|
平均数 |
众数 |
方差 |
|
甲 |
7 |
|
1.2 |
|
乙 |
|
|
2.2 |
(2)如果你是教练,会选择哪位运动员参加比赛?请说明理由。
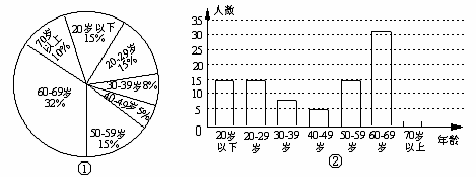
在青岛市政府举办的“迎奥运登山活动”中,参加崂山景区登山活动的市民约有12000人,为统计参加活动人员的年龄情况,我们从中随机抽取了100人的年龄作为样本,进行数据处理,制成扇形统计图和条形统计图(部分)如下:
(1)根据图①提供的信息补全图②;
(2)参加崂山景区登山活动的 12000 余名市民中,哪个年龄段的人数最多?
(3)根据统计图提供的信息,谈谈自己的感想.(不超过30字)
电脑福利彩票中有两种方式“22选5”“29选7”,若选中号码全部正确则获一等奖你认为获一等奖机会大的是
(A)“22选5” (B)“29选7”(C)一样大(D)不能确定
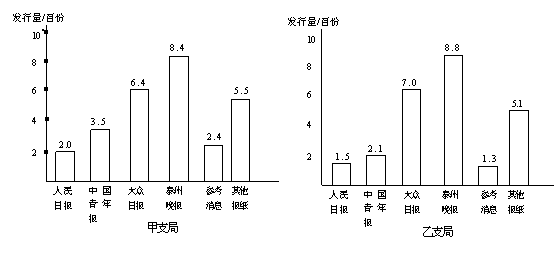 .我市城镇邮政局对甲、乙两个支局的报刊发行部2004年度报纸的发行量进行了统计,并绘成统计图如下:
.我市城镇邮政局对甲、乙两个支局的报刊发行部2004年度报纸的发行量进行了统计,并绘成统计图如下:
请根据上面统计图反映的信息,回答问题:
⑴哪个支局发行《泰州晚报》的份数多?多多少?
⑵分别写出上面两个统计图中提供的6个统计数据的中位数;
⑶已知甲、乙两个支局所服务的居民区住户分别是11280户、8600户,哪个居民区平均每户订阅报纸的份数多?试说明理由。
同时抛掷两枚硬币,按照正面出现的次数,可以分为“2个正面”、“1??个正面”和“没有正面”这3种可能的结果,小红与小明两人共做了6组实验,每组实验都为同时抛掷两枚硬币10次,下表为实验记录的统计表:
|
结果 |
第一组 |
第二组 |
第三组 |
第四组 |
第五组 |
第六组 |
|
两个正面 |
3 |
3 |
5 |
1 |
4 |
2 |
|
一个正面 |
6 |
5 |
5 |
5 |
5 |
7 |
|
没有正面 |
1 |
2 |
0 |
4 |
1 |
1 |
(1) 由上表结果,计算出现“2个正面”、“1个正面”和“没有正面”这3种结果的频率分别是多少?
(2) 从他的实验记录和你自己的生活经验中,你能否对这三种结果的可能性的大小作出预测?并通过树状图进行验证。
(3) 小红与小明约定:只抛一枚硬币,掷出正面小红得1分,掷出反面小明得1分,先得100分的人赢得一个大蛋糕,但因小红有事,游戏中途停止,此时小红得了99分,小明得了98分,问蛋糕应如何分配?
有十五位同学参加智力竞赛,且他们的分数互不相同,取八位同学进入决赛,某人知道了自己的分数后,还需知道这十五位同学的分数的什么量,就能判断他能不能进入决赛( )
A、平均数 B、众数 C、最高分数 D、中位数
18、在“抛一枚均匀硬币”的实验中,如果现在没有硬币,则下面各个试验中哪个不能代替( )
A、两张扑克,“黑桃” 代替“正面”,“红桃” 代替“反面”
B、两个形状大小完全相同,但一红一白的两个乒乓球
C、扔一枚图钉
D、人数均等的男生、女生,以抽签的方式随机抽取一人
夏雪同学调查了班级同学身上有多少零用钱,将每位同学的零用钱记录下来,下面是全班40名同学的零用钱的数目(单位:元)
2,5,0,5,2,5,6,5,0,5,5,52,5,8,0,5,5,2,5,
5,8,6,5,2,5,5,2,5,6,5,5,0,6,5,6,5,2,5,0.
(1)请你写出同学的零用钱(0元,2元,5元,6元8元)出现的频数;
(2)求出同学的零用钱的平均数、中位数和众数;
(3)假如老师随机问一个同学的零用钱,老师最有可能得到的回答是多少元?
某校每学期都要对优秀的学生进行表扬,而每班采取民主投票的方式进行选举,然后把名单报到学校. 若每个班级平均分到3位三好生、4位模范生、5位成绩提高奖的名额,且各项均不能兼得. 现在学校有30个班级,平均每班50人.
(1)作为一名学生,你恰好能得到荣誉的机会有多大?
(2)作为一名学生,你恰好能当选三好生、模范生的机会有多大?
(3)在全校学生数、班级人数、三好生数、模范生数、成绩提高奖人数中,哪些是解决上面两个问题所需要的?
(4)你可以用哪些方法来模拟实验?
(1)0元的频数是5,2元的频数是7,5元的频数是21,6元的频数是5,8元的频数是2.
(2)平均数是4.125,中位数是5,众数是5.
(3)5元.