摘要：如图.已知抛物线的顶点坐标为M.与x轴交于A.B两点.与y轴交于点C. (1)求抛物线的解析式及点A.B.C的坐标, (2)若直线y=kx+t经过C.M两点.且与x轴交于点D.试证明四边形CDAN是平行四边形, (3)点P在抛物线的对称轴x=1上运动.请探索:在x轴上方是否存在这样的P点.使以P为圆心的圆经过A.B两点.并且与直线CD相切.若存在.请求出点P的坐标,若不存在.请说明理由. 解:(1)由抛物线的顶点是M(1.4).设解析式为 又抛物线经过点N(2.3).所以 解得a＝-1 所以所求抛物线的解析式为y＝ 令y＝0.得解得: 得A , 令x＝0.得y＝3.所以 C(0.3). (2)直线y=kx+t经过C.M两点.所以即k＝1.t＝3 直线解析式为y＝x+3. 令y＝0.得x＝-3.故D CD＝ 连接AN.过N做x轴的垂线.垂足为F. 设过A.N两点的直线的解析式为y＝mx+n. 则解得m＝1.n＝1 所以过A.N两点的直线的解析式为y＝x+1 所以DC∥AN. 在Rt△ANF中.AN＝3.NF＝3.所以AN＝ 所以DC＝AN. 因此四边形CDAN是平行四边形. (3)假设在x轴上方存在这样的P点.使以P为圆心的圆经过A.B两点.并且与直线CD相切.设P(1.u) 其中u＞0.则PA是圆的半径且 过P做直线CD的垂线.垂足为Q.则PQ＝PA时以P为圆心的圆与直线CD相切. 由第(2)小题易得:△MDE为等腰直角三角形.故△PQM也是等腰直角三角形. 由P(1.u)得PE＝u. PM＝|4-u|. PQ＝ 由得方程:.解得. 舍去负值u＝ .符合题意的u＝. 所以.满足题意的点P存在.其坐标为(1.).
网址：http://m.1010jiajiao.com/timu3_id_440798[举报]
如图，已知抛物线的顶点坐标为M（1，4），且经过点N（2，3），与x轴交于A、B两点（点A在点B左侧），与y轴交于点C．（1）求抛物线的解析式及点A、B、C的坐标；
（2）直线AN交y轴于点F，P是抛物线的对称轴x=1上动点，H是X轴上一动点，请探索：是否存在这样的P、H，使四边形CFHP的周长最短？若存在，请求出四边形CFHP的最短周长和点P、H的坐标；若不存在，请说明理由；
（3）若点Q是∠MDB的角平分线上动点，点R是线段DB上的动点，Q、R在何位置时，BQ+QR的值最小．请直接写出BQ+QR的最小值和Q、R的坐标．
如图，已知抛物线的顶点坐标为M（1，4），与x轴交于A、B两点（点A在点B左侧），与y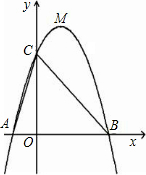
轴交于点C（0，3）．
（1）求抛物线的解析式；
（2）求tan∠ACO与sin∠BCO的乘积；
（3）在线段BC边上是否存在点P，使得以B、O、P为顶点的三角形与△BAC相似？若存在，求出点P的坐标；若不存在，请说明理由．
（4）在对称轴上是否存在一点P，使|PC-PB|的值最大，请求出点P的坐标． 查看习题详情和答案>>
轴交于点C（0，3）．（1）求抛物线的解析式；
（2）求tan∠ACO与sin∠BCO的乘积；
（3）在线段BC边上是否存在点P，使得以B、O、P为顶点的三角形与△BAC相似？若存在，求出点P的坐标；若不存在，请说明理由．
（4）在对称轴上是否存在一点P，使|PC-PB|的值最大，请求出点P的坐标． 查看习题详情和答案>>
如图，已知抛物线的顶点为M（5，6），且经过点C（-1，0）．
（1）求抛物线的解析式；
（2）设抛物线与y轴交于点A，过A作AB∥x轴，交抛物线于另一点B，则抛物线上存在点P，使△ABP的面积等于△ABO的面积，请求出所有符合条件的点P的坐标；
（3）将抛物线向右平移，使抛物线经过点（5，0），请直接答出曲线段CM（抛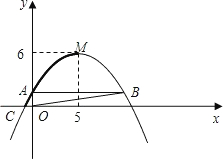
物线图象的一部分，如图中的粗线所示）在平移过程中所扫过的面积．
查看习题详情和答案>>
（1）求抛物线的解析式；
（2）设抛物线与y轴交于点A，过A作AB∥x轴，交抛物线于另一点B，则抛物线上存在点P，使△ABP的面积等于△ABO的面积，请求出所有符合条件的点P的坐标；
（3）将抛物线向右平移，使抛物线经过点（5，0），请直接答出曲线段CM（抛
物线图象的一部分，如图中的粗线所示）在平移过程中所扫过的面积．
查看习题详情和答案>>
于A、B两点（点A在点B左侧），与y轴交于点C．
如图，已知抛物线的顶点A在y轴上，坐标A（0，1）矩形CDEF的顶点C、F在抛物线上，D、E在x轴上，CF交y轴于点B（0，2），S矩形CDEF=8