第十六讲 圆锥曲线的定义、性质和方程(一)
★★★高考在考什么
【考题回放】
1.已知AB为过抛物线y2=2px焦点F的弦, 则以AB为直径的圆与抛物线的准线(B)
A.相交 B.相切 C.相离 D.与p的取值有关
2.(江苏理)在平面直角坐标系xOy中,双曲线中心在原点,焦点在y轴上,一条渐近线方程为x-2y=0,则它的离心率为 ( A )
A. B.
B. C.
C. D.
D.
3.点P(a,b)是双曲线x2-y2=1右支上一点,且P到渐近线距离为 ,则a+b=(B )
,则a+b=(B )
A、- B、
B、 C、-2 D、2
C、-2 D、2
4.(湖南)设F1 、F2分别是椭圆 (
( )的左、右焦点,若在其右准线上存在P使线段PF1的中垂线过点F2,则椭圆离心率的取值范围是( D
)
)的左、右焦点,若在其右准线上存在P使线段PF1的中垂线过点F2,则椭圆离心率的取值范围是( D
)
A. B.
B. C.
C. D.
D.
5.(湖北理)双曲线 的左准线为l,左焦点和右焦点分别为F1 、F2;抛物线C2的准线为l,焦点为F2;C1与C2的一个交点为M,则
的左准线为l,左焦点和右焦点分别为F1 、F2;抛物线C2的准线为l,焦点为F2;C1与C2的一个交点为M,则 等于
( A )
等于
( A )
A. B.
B. C.
C. D.
D.
6.(全国一)抛物线y2=4x的焦点为F,准线为l,经过F且斜率为 的直线与抛物线在x轴上方的部分相交于点A,AK^l,垂足为K,则△AKF的面积是( C)
的直线与抛物线在x轴上方的部分相交于点A,AK^l,垂足为K,则△AKF的面积是( C)
A.4
B. C.
C. D.8
D.8
7.(福建理)以双曲线 的右焦点为圆心,且与其渐近线相切的圆方程是
(
A )
的右焦点为圆心,且与其渐近线相切的圆方程是
(
A )
A.x2+y2-10x+9=0 B.x2+y2-10x+16=
8.(辽宁)设椭圆 上一点P到左准线的距离为10,F是该椭圆的左焦点,若点M满足
上一点P到左准线的距离为10,F是该椭圆的左焦点,若点M满足 ,则
,则 2
2
★★★高考要考什么
【热点透析】
一、圆锥曲线的定义
1. 椭圆:到两个定点的距离之和等于定长(定长大于两个定点间的距离)的动点的轨迹叫做椭圆。即:{P| |PF1|+|PF2|=
2. 双曲线:到两个定点的距离的差的绝对值为定值(定值小于两个定点的距离)的动点轨迹叫做双曲线。即{P| ||PF1|-|PF2||=
3. 圆锥曲线的统一定义:到定点的距离与到定直线的距离的比e是常数的点的轨迹叫做圆锥曲线。当0<e<1时为椭圆:当e=1时为抛物线;当e>1时为双曲线。
二、圆锥曲线的方程。
1.椭圆: (a>b>0)或
(a>b>0)或 (a>b>0)(其中,a2=b2+c2)
(a>b>0)(其中,a2=b2+c2)
2.双曲线: (a>0, b>0)或
(a>0, b>0)或 (a>0, b>0)(其中,c2=a2+b2)
(a>0, b>0)(其中,c2=a2+b2)
3.抛物线:y2=±2px(p>0),x2=±2py(p>0)
三、圆锥曲线的性质
知识要点:
1.椭圆: (a>b>0)
(a>b>0)
(1)范围:|x|≤a,|y|≤b (2)顶点:(±a,0),(0,±b) (3)焦点:(±c,0)
(4)离心率:e=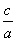 ∈(0,1) (5)准线:
∈(0,1) (5)准线:
2.双曲线: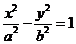 (a>0, b>0)
(a>0, b>0)
(1)范围:|x|≥a, y∈R (2)顶点:(±a,0)
(3)焦点:(±c,0)
(4)离心率: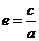 ∈(1,+∞) (5)准线:
∈(1,+∞) (5)准线: (6)渐近线:
(6)渐近线: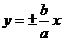
3.抛物线:y2=2px(p>0)
(1)范围:x≥0, y∈R (2)顶点:(0,0)
(3)焦点:(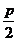 ,0)
,0)
(4)离心率:e=1
(5)准线:x=-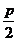
主要题型:
(1)定义及简单几何性质的灵活运用;
(2)求曲线方程(含指定圆锥曲线方程及轨迹方程)。
★★★突破重难点
【例1】若F1、F2为双曲线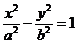 的左、右焦点,O为坐标原点,点P在双曲线的左支上,点M在双曲线的右准线上,且满足:
的左、右焦点,O为坐标原点,点P在双曲线的左支上,点M在双曲线的右准线上,且满足:
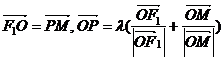
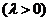 ,
,
则该双曲线的离心率为( )
A.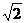 B.
B. C.
C. D.3
D.3
解:由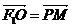 知四边形F1OMP是平行四边形,又
知四边形F1OMP是平行四边形,又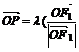
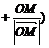
知OP平分∠F1OM,即F1OMP是菱形,设|OF1|=c,则|PF1|=c.
又|PF2|-|PF1|=
由双曲线的第二定义知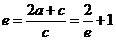 ,且e>1,∴e=2,故选C.
,且e>1,∴e=2,故选C.
【例2】学校科技小组在计算机上模拟航天器变轨返回试验. 设计方案如图:航天器运行(按顺时针方向)的轨迹方程为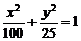 ,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以
,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以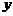 轴为对称轴、
轴为对称轴、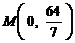 为顶点的抛物线的实线部分,降落点为
为顶点的抛物线的实线部分,降落点为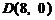 . 观测点
. 观测点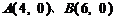 同时跟踪航天器.
同时跟踪航天器.
(1)求航天器变轨后的运行轨迹所在的曲线方程;
(2)试问:当航天器在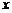 轴上方时,观测点
轴上方时,观测点 测得离航天器的距离分别为多少时,应向航天器发出变轨指令?
测得离航天器的距离分别为多少时,应向航天器发出变轨指令?
解:(1)设曲线方程为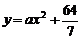 , 由题意可知,
, 由题意可知,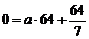 .
. 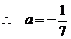 .
.

 曲线方程为
曲线方程为 .
.
(2)设变轨点为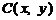 ,根据题意可知
,根据题意可知
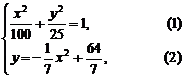
得 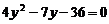 ,
,
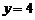 或
或 (不合题意,舍去).
(不合题意,舍去).
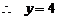 .
.
得 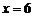 或
或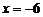 (不合题意,舍去).
(不合题意,舍去).
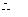
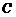 点的坐标为
点的坐标为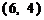 ,
,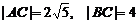 .
.
答:当观测点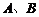 测得
测得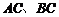 距离分别为
距离分别为 时,应向航天器发出指令.
时,应向航天器发出指令.
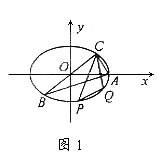 【例3】如图1,已知A、B、C是长轴为4的椭圆上三点,点A是长轴的一个顶点,BC过椭圆中心O,且
【例3】如图1,已知A、B、C是长轴为4的椭圆上三点,点A是长轴的一个顶点,BC过椭圆中心O,且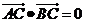 ,
,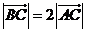 。
。
(1)建立适当的坐标系,求椭圆方程;
(2)如果椭圆上两点P、Q使直线CP、CQ与x轴围
成底边在x轴上的等腰三角形,是否总存在实数l
使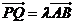 ?请给出证明。
?请给出证明。
解:(1)以O为原点,OA所在的直线为x轴建立如
图直角坐标系,则A(2,0),椭圆方程可设为
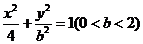 。
。
而O为椭圆中心,由对称性知|OC|=|OB|
又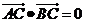 ,所以AC⊥BC
,所以AC⊥BC
又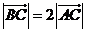 ,所以|OC|=|AC|,
,所以|OC|=|AC|,
所以△AOC为等腰直角三角形,所以点C坐标为(1,1)。将(1,1)代入椭圆方程得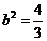 ,则椭圆方程为
,则椭圆方程为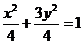 。
。
(2)由直线CP、CQ与x轴围成底边在x轴上的等腰三角形,设直线CP的斜率为k,则直线CQ的斜率为-k,直线CP的方程为y-1=k(x-1),直线CQ的方程为y-1=-k(x-1)。由椭圆方程与直线CP的方程联立,消去y得
(1+3k2)x2-6k(k-1)x+3k2-6k-1=0①
因为C(1,1)在椭圆上,所以x=1是方程①的一个根,于是
 同理
同理
这样, ,
又B(-1,-1),所以
,
又B(-1,-1),所以 ,
,
即kAB=kPQ。所以PQ∥AB,存在实数l使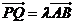 。
。
 【例4】如图,直线l1和l2相交于点M,l1
⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=
【例4】如图,直线l1和l2相交于点M,l1
⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=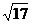 ,|AN|=3,且|BN|=6.建立适当的坐标系,求曲线C的方程.
,|AN|=3,且|BN|=6.建立适当的坐标系,求曲线C的方程.
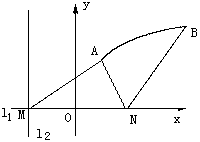
解法一:如图建立坐标系,以l1为x轴,MN的垂直平分线为y轴,点O为坐标原点.
依题意知:曲线段C是以点N为焦点,以l2为准线的抛线段的一段,其中A、B分别为C的端点.设曲线段C的方程为
y2=2px (p>0),(xA≤x≤xB,y>0),其中xA,xB分别为A,B的横坐标,P=|MN|.
 所以 M (-
所以 M (-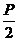 ,0),N (
,0),N (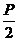 ,0).
,0).
由 |AM|=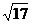 ,|AN|=3得
,|AN|=3得
(xA+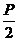 )2+2PxA=17, ①
)2+2PxA=17, ①
(xA-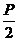 )2+2PxA=9. ②
)2+2PxA=9. ②
由①、②两式联立解得xA= ,再将其代入①式并由p>0解得
,再将其代入①式并由p>0解得
 或
或 .
.
因为△AMN是锐角三角形,所以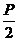 >xA,故舍去
>xA,故舍去 .
.
∴ P=4,xA=1.
由点B在曲线段C上,得xB=|BN|-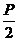 =4.
=4.
综上得曲线段C的方程为y2=8x (1≤x≤4,y>0).
解法二:如图建立坐标系,分别以l1、l2为x、y轴,M为坐标原点.
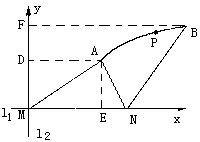 作AE⊥l1,AD⊥l2,BF⊥l2,垂足分别为E、D、F.
作AE⊥l1,AD⊥l2,BF⊥l2,垂足分别为E、D、F.
设 A (xA,yA)、B (xB,yB)、N (xN,0).
依题意有
xA=|ME|=|DA|=|AN|=3,
yA=|DM|= =2
=2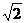 ,由于△AMN为锐角三角形,故有
,由于△AMN为锐角三角形,故有
xN=|AE|+|EN|=4.
=|ME|+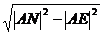 =4
=4
XB=|BF|=|BN|=6.
设点P (x,y)是曲线段C上任一点,则由题意知P属于集合
{(x,y)|(x-xN)2+y2=x2,xA≤x≤xB,y>0}.
故曲线段C的方程
y2=8(x-2)(3≤x≤6,y>0).
第十七讲 圆锥曲线的定义、性质和方程(二)
【例5】已知椭圆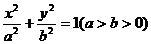 的长、短轴端点分别为A、B,从此椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点F1,向量
的长、短轴端点分别为A、B,从此椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点F1,向量 与
与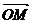 是共线向量。
是共线向量。
(1)求椭圆的离心率e;
(2)设Q是椭圆上任意一点, F1、F2分别是左、右焦点,求∠F1QF2的取值范围;
解:(1)∵ ,∴
,∴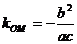 。
。
∵ 是共线向量,∴
是共线向量,∴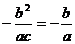 ,∴b=c,故
,∴b=c,故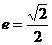 。
。
(2)设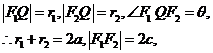
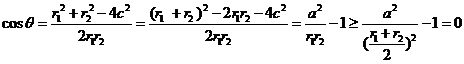
当且仅当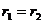 时,cosθ=0,∴θ
时,cosθ=0,∴θ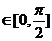 。
。
(1)过点P分别作两渐近线的垂线,垂足分别为E,F,求 的值;
的值;
(2)过点P的直线与两渐近线分别交于A、B两点,且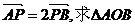 的面积.
的面积.
|

 右支上任一点.
右支上任一点.
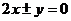
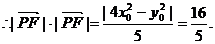
 ,
,

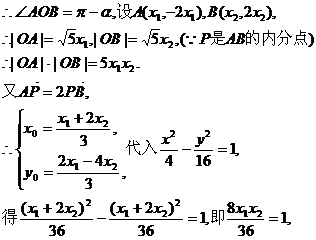
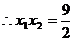
 所成的比为
所成的比为 ,双曲线过C、D、E三点,且以A、B为焦点.求双曲线的离心率.
,双曲线过C、D、E三点,且以A、B为焦点.求双曲线的离心率.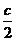 ,h),B(c,0),其中c为双曲线的半焦距,c=
,h),B(c,0),其中c为双曲线的半焦距,c= |AB|,h是梯形的高.
|AB|,h是梯形的高.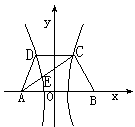 由定比分点坐标公式,得点E的坐标为
由定比分点坐标公式,得点E的坐标为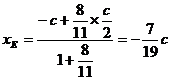 ,
,  .
.  ,则离心率
,则离心率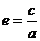 .
.
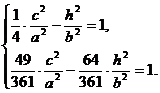
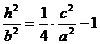 代入②式得
代入②式得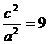 所以,离心率
所以,离心率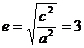
 ,
, ,
,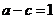 ,
,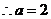 ,
,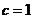 ,
,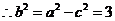

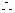 椭圆的标准方程为
椭圆的标准方程为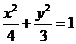
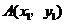 ,
, ,
,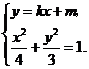 得
得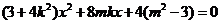 ,
,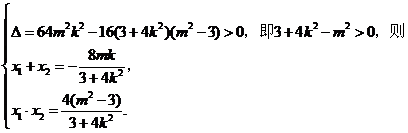
 ,
,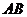 为直径的圆过椭圆的右顶点
为直径的圆过椭圆的右顶点 ,
, ,即
,即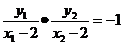 ,
,
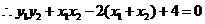 ,
,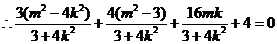 ,
,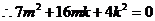
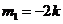 ,
, ,且均满足
,且均满足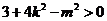 ,
,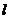 的方程为
的方程为 ,直线过定点
,直线过定点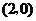 ,与已知矛盾;
,与已知矛盾; ,直线过定点
,直线过定点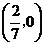
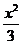 +y2=1上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是(C )
+y2=1上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是(C )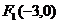 、
、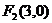 ,一条渐近线方程为
,一条渐近线方程为 ,那么它的两条准线间的距离是( C )
,那么它的两条准线间的距离是( C )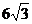 B.
B.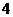 C.
C.
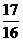 (
B )
(
B )  (
C )
(
C ) 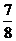 (
D ) 0
(
D ) 0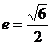 ,F1、F2分别是它的左,右焦点,若过F1的直线与双曲线的左支交于A、B两点,且|AB|是|AF2|与|BF2|的等差中项,则|AB|为(A).
,F1、F2分别是它的左,右焦点,若过F1的直线与双曲线的左支交于A、B两点,且|AB|是|AF2|与|BF2|的等差中项,则|AB|为(A).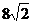 B、
B、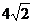 C、
C、 D、8
D、8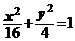 .
.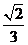 (B)
(B) 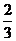 (C)
(C) 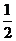 (D)
(D)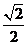
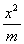 +
+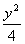 =1的离心率e=
=1的离心率e=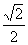 ,则m=___________m=8或2。
,则m=___________m=8或2。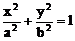 (a>b>0)的两焦点,过F1的弦AB与F2组成等腰直角三角形ABF2,其中∠BAF2=900,则椭圆的离心率是________
(a>b>0)的两焦点,过F1的弦AB与F2组成等腰直角三角形ABF2,其中∠BAF2=900,则椭圆的离心率是________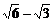
 9.已知椭圆E的离心率为e,左、右焦点为F1、F2,抛物线C以F2为焦点,F1为其顶点,若P为两曲线的公共点,且e|PF2|=|PF1|,则e=__________。
9.已知椭圆E的离心率为e,左、右焦点为F1、F2,抛物线C以F2为焦点,F1为其顶点,若P为两曲线的公共点,且e|PF2|=|PF1|,则e=__________。

 ;
; 。
。
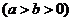 上的一个动点,弦AB、AC分别过焦点F1、F2.当AC垂直于x轴 时,恰好|AF1|:|AF2=3:1
上的一个动点,弦AB、AC分别过焦点F1、F2.当AC垂直于x轴 时,恰好|AF1|:|AF2=3:1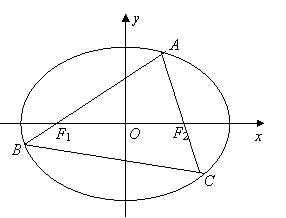 (II)设
(II)设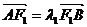 ,
,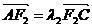 ,试判断l1+l2是否为定值?若是,则求出该定值;若不是,请说明理由.
,试判断l1+l2是否为定值?若是,则求出该定值;若不是,请说明理由.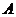 C垂直于x轴时,
C垂直于x轴时,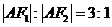 ,由
,由 ,
, ,
,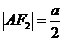
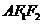 中,
中,
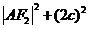
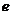 =
= ,则
,则 ,
,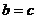 .
.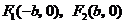 ,则椭圆方程为
,则椭圆方程为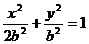 ,
,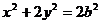 .
.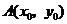 ,
, ,
,
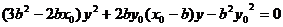 .
.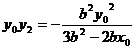 ,∴
,∴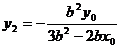
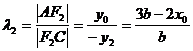 ,同理可得
,同理可得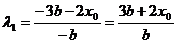
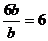 .
. 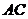
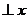 轴,
轴, ,
,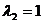 ,
,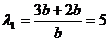
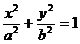 (a>b>0)上两点A、B,直线
(a>b>0)上两点A、B,直线 上有两点C、D,且ABCD是正方形。此正方形外接圆为x2+y2-2y-8=0,求椭圆方程和直线
上有两点C、D,且ABCD是正方形。此正方形外接圆为x2+y2-2y-8=0,求椭圆方程和直线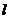 的方程。
的方程。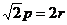 ,∴
,∴ ,又O'是正方形ABCD的中心,∴O'到直线y=x+k的距离应等于正方形边长p的一半即
,又O'是正方形ABCD的中心,∴O'到直线y=x+k的距离应等于正方形边长p的一半即 ,由点到直线的距离公式可知k=-2或k=4。
,由点到直线的距离公式可知k=-2或k=4。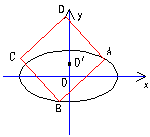
 (1)设AB:y=x-2 由 y=x-2
(1)设AB:y=x-2 由 y=x-2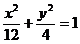 。
。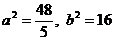 ,此时b2>a2(舍去)。
,此时b2>a2(舍去)。