摘要：XB=|BF|=|BN|=6． 设点P (x.y)是曲线段C上任一点.则由题意知P属于集合{(x.y)|(x-xN)2+y2=x2.xA≤x≤xB.y＞0}． 故曲线段C的方程y2=8(x-2)(3≤x≤6.y＞0)． 第十七讲 圆锥曲线的定义.性质和方程(二)
网址：http://m.1010jiajiao.com/timu_id_528743[举报]
已知点P在曲线C：y=
（x＞1）上，设曲线C在点P处的切线为l，若l与函数y=kx（k＞0）的图象的交点为A，与x轴的交点为B，设点P的横坐标为t，A、B的横坐标分别为xA、xB，记f（t）=xA•xB．
（Ⅰ）求f（t）的解析式；
（Ⅱ）设数列{an}（n≥1，n∈N）满足a1=1，an=f(
)（n≥2），数列{bn}满足bn=
-
，求an与bn；
（Ⅲ）在（Ⅱ）的条件下，当1＜k＜3时，证明不等式：a1+a2+…+an＞
．
查看习题详情和答案>>
| 1 |
| x |
（Ⅰ）求f（t）的解析式；
（Ⅱ）设数列{an}（n≥1，n∈N）满足a1=1，an=f(
| an-1 |
| 1 |
| an |
| k |
| 3 |
（Ⅲ）在（Ⅱ）的条件下，当1＜k＜3时，证明不等式：a1+a2+…+an＞
| 3n-8k |
| k |
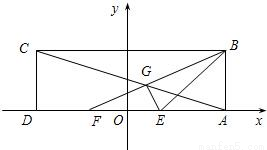
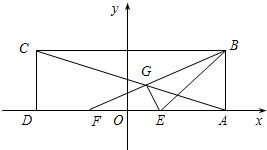在矩形ABCD中，已知AD=6，AB=2，E、F为AD的两个三等分点，AC和BF交于点G，△BEG的外接圆为⊙H．以DA所在直线为x轴，以DA中点O为坐标原点，建立如图所示的平面直角坐标系．（1）求以F、E为焦点，DC和AB所在直线为准线的椭圆的方程．
（2）求⊙H的方程．
（3）设点P（0，b），过点P作直线与⊙H交于M，N两点，若点M恰好是线段PN的中点，求实数b的取值范围． 查看习题详情和答案>>
已知点P在曲线C：y=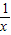
（x＞1）上，设曲线C在点P处的切线为l，若l与函数y=kx（k＞0）的图象的交点为A，与x轴的交点为B，设点P的横坐标为t，A、B的横坐标分别为xA、xB，记f（t）=xA•xB．
（Ⅰ）求f（t）的解析式；
（Ⅱ）设数列{an}（n≥1，n∈N）满足a1=1，an=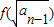
（n≥2），数列{bn}满足bn=
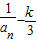，求an与bn；
（Ⅲ）在（Ⅱ）的条件下，当1＜k＜3时，证明不等式：a1+a2+…+an＞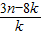
．
查看习题详情和答案>>
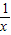（x＞1）上，设曲线C在点P处的切线为l，若l与函数y=kx（k＞0）的图象的交点为A，与x轴的交点为B，设点P的横坐标为t，A、B的横坐标分别为xA、xB，记f（t）=xA•xB．（Ⅰ）求f（t）的解析式；
（Ⅱ）设数列{an}（n≥1，n∈N）满足a1=1，an=
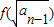（n≥2），数列{bn}满足bn=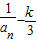，求an与bn；（Ⅲ）在（Ⅱ）的条件下，当1＜k＜3时，证明不等式：a1+a2+…+an＞
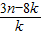．查看习题详情和答案>>
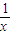（x＞1）上，设曲线C在点P处的切线为l，若l与函数y=kx（k＞0）的图象的交点为A，与x轴的交点为B，设点P的横坐标为t，A、B的横坐标分别为xA、xB，记f（t）=xA•xB．
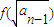（n≥2），数列{bn}满足bn=
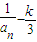，求an与bn；
．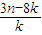